Nuclear fission and nuclear fusion are different types of reactions that release energy (when exothermic) due to the formation of nuclei with higher nuclear binding energy.
- Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei).
- Nuclear fusion is a nuclear reaction in which two or more atomic nuclei collide at very high energy and fuse together into a new nucleus.
This is the main difference. Whether the reaction is exothermic or not depends on the binding energy of the resulting nuclei.
Nuclear Fission
Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission process often produces free neutrons and photons (in the form of gamma rays) and releases a large amount of energy. Nuclear fission is either a nuclear reaction or a radioactive decay process in nuclear physics. The decay process is called spontaneous fission, and it is a very rare process. In reactor physics, neutron-induced nuclear fission is the process of the greatest practical importance.
The total energy released in fission can be calculated from binding energies of the initial target nucleus to be fissioned and binding energies of fission products. But not all the total energy can be recovered in a reactor.
Nuclear Fusion
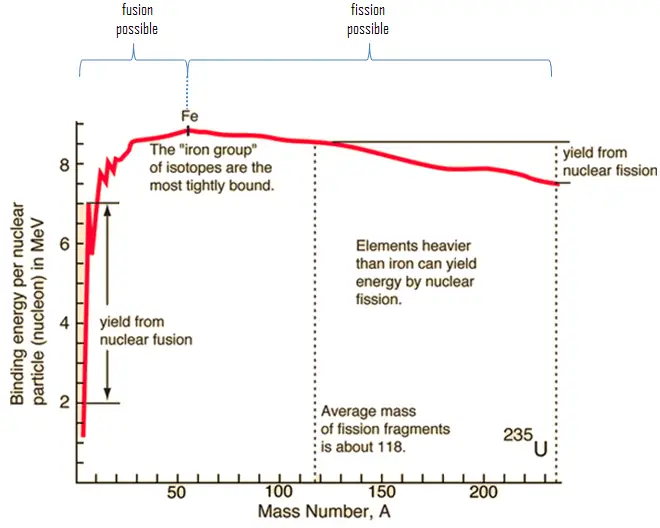
In nuclear physics, nuclear fusion is a nuclear reaction in which two or more atomic nuclei collide at very high energy and fuse together into a new nucleus, e.g., helium. If light nuclei are forced together, they will fuse with a yield of energy because the mass of the combination will be less than the sum of the masses of the individual nuclei. Suppose the combined nuclear mass is less than that of iron at the peak of the binding energy curve. In that case, the nuclear particles will be more tightly bound than they were in the lighter nuclei, and that decrease in mass comes off in the form of energy, according to the Albert Einstein relationship. For elements like uranium and thorium, fission will yield energy. Fusion reactions have an energy density many times greater than nuclear fission, and fusion reactions are millions of times more energetic than chemical reactions.
Nuclear Fission vs Fusion – Reactions
Uranium – 235 Fission
Uranium 235 is a fissile isotope, and its fission cross-section for thermal neutrons is about 585 barns (for 0.0253 eV neutron). For fast neutrons, its fission cross-section is on the order of barns. Most absorption reactions result in fission reactions, but a minority results in radiative capture forming 236U. The cross-section for radiative capture for thermal neutrons is about 99 barns (for 0.0253 eV neutron). Therefore about 15% of all absorption reactions result in radiative capture of neutrons. About 85% of all absorption reactions result in fission.
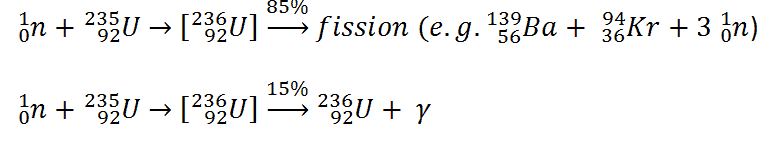
The average of the fragment mass is about 118, but very few fragments near that average are found. It is much more probable to break up into unequal fragments, and the most probable fragment masses are around mass 95 (Krypton) and 137 (Barium).
Most of these fission fragments are highly unstable (radioactive) and undergo further radioactive decays to stabilize itself. Fission fragments interact strongly with the surrounding atoms or molecules traveling at high speed, causing them to ionize.
Most energy released by one fission (~160MeV of total ~200MeV) appears as kinetic energy of the fission fragments.
Deuterium-Tritium Fusion
The fusion reaction of deuterium and tritium is particularly interesting because of its potential of providing energy for the future.
3T (d, n) 4He
The reaction yields ~17 MeV of energy per reaction. Still, it requires an enormous temperature of approximately 40 million Kelvins to overcome the coulomb barrier by the attractive nuclear force, stronger at close distances. The deuterium fuel is abundant, but tritium must be either bred from lithium or gotten in the operation of the deuterium cycle.
The Q-value of this reaction can be calculated from the atom masses of the reactants and products:
m(3T) = 3.0160 amu
m(2D) = 2.0141 amu
m(1n) = 1.0087 amu
m(4He) = 4.0026 amu
Using the mass-energy equivalence, we get the Q-value of this reaction as:
Q = {(3.0160+2.0141) [amu] – (1.0087+4.0026) [amu]} x 931.481 [MeV/amu]
= 0.0188 x 931.481 = 17.5 MeV
See also: Q-value
Nuclear Fission vs Fusion – Examples
Fission Powers Nuclear Reactors
In general, nuclear fission results in the release of enormous quantities of energy. This energy can be used in nuclear power plants to produce electricity or process heat. A typical nuclear power plant has an electric-generating capacity of 1000 MWe. The heat source in the nuclear power plant is a nuclear reactor. As is typical in all conventional thermal power stations, the heat is used to generate steam which drives a steam turbine connected to a generator that produces electricity. The turbines are heat engines subject to the efficiency limitations imposed by the second law of thermodynamics. In modern nuclear power plants, the overall thermodynamic efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power.
This thermal power is generated in a reactor core, especially the nuclear fuel (fuel assemblies), the moderator, and the control rods. The reactor’s core contains all the nuclear fuel assemblies and generates most of the heat (fraction of the heat is generated outside the reactor – e.g., gamma rays energy). According to a fuel loading pattern, the assemblies are exactly placed in the reactor.
Consumption of a 3000MWth (~1000MWe) reactor (12-months fuel cycle):
- The annual natural uranium consumption of this reactor is about 250 tonnes of natural uranium (to produce about 25 tonnes of enriched uranium).
- The annual enriched uranium consumption of this reactor is about 25 tonnes of enriched uranium.
- The annual fissile material consumption of this reactor is about 1 005 kg.
- The annual matter consumption of this reactor is about 1.051 kg.
Fusion Powers the Sun
The Sun is a hot star. Really hot star. But all of the heat and light coming from the Sun comes from the fusion reactions happening inside the core of the Sun. Inside the Sun, the pressure is millions of times more than the surface of the Earth, and the temperature reaches more than 15 million Kelvin. Massive gravitational forces create these conditions for nuclear fusion. On Earth, it is impossible to achieve such conditions.
The Sun burns hydrogen atoms, which fuse together to form helium nuclei, and a small amount of matter is converted into energy. The Sun consumes approximately 620 million metric tons of hydrogen each second at its core. Hydrogen, heated to very high temperatures, changes its state from a gaseous state to a plasma state. Normally, fusion is not possible because the strongly repulsive electrostatic forces between the positively charged nuclei prevent them from getting close enough together to collide and for fusion to occur. The mechanism, how to overcome the coulomb barrier is by the temperature and by the pressure. The attractive nuclear force allows the nuclei to fuse together at close distances.