Prompt Neutron Lifetime
Prompt neutron lifetime, l, is the average time from a prompt neutron emission to its absorption (fission or radiative capture) or its escape from the system. This parameter is defined in multiplying or also in non-multiplying systems. In both systems the prompt neutron lifetimes depend strongly on:
- the material composition of the system
- multiplying – non-multiplying system
- the system with or without thermalization
- isotopic composition of the system
- the geometric configuration of the system
- homogeneous or heterogeneous system
- the shape of the entire system
- size of the system
In an infinite reactor (without escape), prompt neutron lifetime is the sum of the slowing downtime and the diffusion time.
l=ts + td
In an infinite thermal reactor ts << td and therefore l ≈ td. The typical prompt neutron lifetime in thermal reactors is on the order of 10−4 seconds. Generally, the longer neutron lifetimes occur in systems in which the neutrons must be thermalized to be absorbed.
Most neutrons are absorbed in higher energies, and the neutron thermalization is suppressed (e.g.,, in fast reactors), have much shorter prompt neutron lifetimes. The typical prompt neutron lifetime in fast reactors is on the order of 10−7 seconds.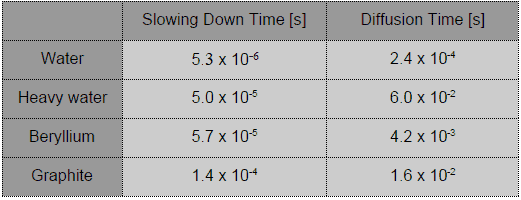
Slowing Down and Diffision Times for Thermal Neutrons in an Infinite Medium
Source: Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
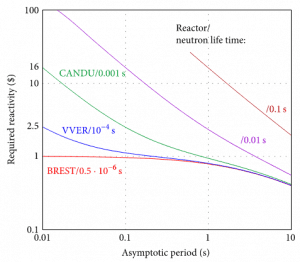Dependencies of asymptotic time period on the reactivity required for different reactor types with different prompt neutron lifetimes. Source: http://www.hindawi.com/journals/ijne/2014/373726/
Example – Infinite Multiplying System Without Source and Delayed Neutrons
An equation governing the neutron kinetics of the system without source and with the absence of delayed neutrons is the point kinetics equation (in a certain form). This equation states that the time change of the neutron population is equal to the excess of neutron production (by fission) minus neutron loss by absorption in one prompt neutron lifetime. The role of prompt neutron lifetime is evident. Shorter lifetimes give simply faster responses to multiplying systems.
If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest form of point kinetics equation (without source and delayed neutrons):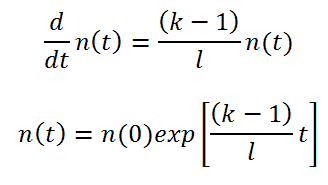
Let us consider that the prompt neutron lifetime is ~2 x 10-5 and k (k∞ – neutron multiplication factor) will be step increased by only 0.01% (i.e., 10pcm or ~1.5 cents), that is k∞=1.0000 will increase to k∞=1.0001.
It must be noted such reactivity insertion (10pcm) is very small in case of LWRs. The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case the reactor period will be:
T = l / (k∞ – 1) = 2 x 10-5 / (1.0001 – 1) = 0.2s
This is a very short period. In one second, the reactor’s neutron flux (and power) would increase by a factor of e5 = 2.7185. In 10 seconds, the reactor would pass through 50 periods, and the power would increase by e50 = ……
Furthermore, in the case of fast reactors in which prompt neutron lifetimes are of the order of 10-7 seconds, the response of such a small reactivity insertion will be even more unimaginable. In the case of 10-7, the period will be:
T = l / (k∞ – 1) = 10-7 / (1.0001 – 1) = 0.001s
Reactors with such kinetics would be very difficult to control. Fortunately, this behavior is not observed in any multiplying system. Actual reactor periods are observed to be considerably longer than computed above, and therefore the nuclear chain reaction can be controlled more easily. The longer periods are observed due to the presence of the delayed neutrons.
Interactive chart – Infinite Multiplying System Without Source and Delayed Neutrons
Press the “clear and run” button and try to stabilize the power at 90%.
Look at the reactivity insertion you need to insert to stabilize the system (of the order to the tenth of pcm).
Do you think that such a system is controlable?
