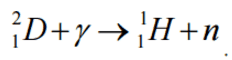In nuclear and particle physics, the energetics of nuclear reactions are determined by the reaction’s Q-value. The Q-value of the reaction is defined as the difference between the sum of the masses of the initial reactants and the sum of the masses of the final products in energy units (usually in MeV).
Consider a typical reaction in which the projectile a and target A give place to two products, B and b. This can also be expressed in the notation we have used, a + A → B + b, or even in a more compact notation, A(a,b)B.
See also: E=mc2
The Q-value of this reaction is given by:
Q = [ma + mA – (mb + mB)]c2
which is the same as the excess kinetic energy of the final products:
Q = Tfinal – Tinitial
= Tb + TB – (Ta + TA)
For reactions in which there is a decrease in the kinetic energy of the products, Q is negative. The negative Q reactions are endothermic (or endoergic), and they require net energy input.
See also: Q-value Calculator
Example of Endothermic Reaction – Photoneutrons
In nuclear reactors, gamma radiation plays a significant role also in reactor kinetics and subcriticality control, especially in nuclear reactors with D2O moderator (CANDU reactors) or with Be reflectors (some experimental reactors). Neutrons can also be produced in (γ, n) reactions, and therefore they are usually referred to as photoneutrons.
A high-energy photon (gamma-ray) can, under certain conditions, eject a neutron from a nucleus. It occurs when its energy exceeds the binding energy of the neutron in the nucleus. Most nuclei have binding energies in excess of 6 MeV, above the energy of most gamma rays from fission. On the other hand, there are few nuclei with a sufficiently low binding energy of practical interest. These are 2D, 9Be, 6Li, 7Li, and 13C. As can be seen from the table, the lowest threshold have 9Be with 1.666 MeV and 2D with 2.226 MeV.
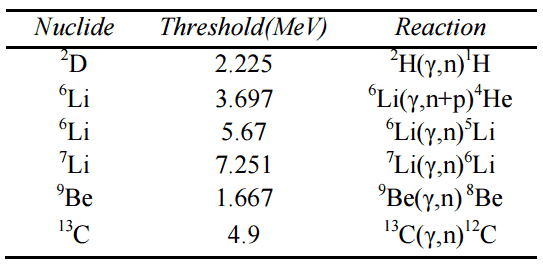
threshold energies.
In the case of deuterium, neutrons can be produced by the interaction of gamma rays (with a minimum energy of 2.22 MeV) with deuterium:
The reaction Q-value is calculated below:
The atom masses of the reactant and products are:
m(2D) = 2.01363 amu
m(1n) = 1.00866 amu
m(1H) = 1.00728 amu
Using the mass-energy equivalence, we get the Q-value of this reaction as:
Q = {2.01363 [amu] – (1.00866+1.00728) [amu]} x 931.481 [MeV/amu]
= -0.00231 x 931.481 = -2.15 MeV
Example: Endothermic Reaction – (α,n) reaction
Calculate the reaction Q-value of the following reaction:
7Li (α, n) 10B
The atom masses of the reactants and products are:
m(4He) = 4.0026 amu
m(7Li) = 7.0160 amu
m(1n) = 1.0087 amu
m(10B) = 10.01294 amu
Using the mass-energy equivalence, we get the Q-value of this reaction as:
Q = {(7.0160+4.0026) [amu] – (1.0087+10.01294) [amu]} x 931.481 [MeV/amu]
= 0.00304 x 931.481 = -2.83 MeV