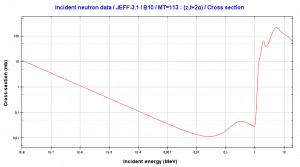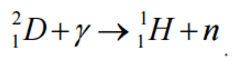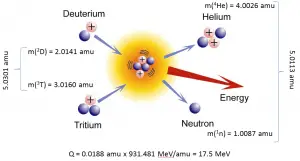
In nuclear and particle physics, the energetics of nuclear reactions is determined by the Q-value of that reaction. The Q-value of the reaction is defined as the difference between the sum of the masses of the initial reactants and the sum of the masses of the final products in energy units (usually in MeV).
Consider a typical reaction in which the projectile a and target A give place to two products, B and b. This can also be expressed in the notation we have used, a + A → B + b, or even in a more compact notation, A(a,b)B.
See also: E=mc2
The Q-value of this reaction is given by:
Q = [ma + mA – (mb + mB)]c2
which is the same as the excess kinetic energy of the final products:
Q = Tfinal – Tinitial
= Tb + TB – (Ta + TA)
For reactions in which there is an increase in the kinetic energy of the products, Q is positive. The positive Q reactions are said to be exothermic (or exergic). There is a net release of energy since the kinetic energy of the final state is greater than the kinetic energy of the initial state.
For reactions in which there is a decrease in the kinetic energy of the products, Q is negative. The negative Q reactions are endothermic (or endoergic), and they require net energy input.