A magic number is a number of nucleons in a nucleus, corresponding to complete shells within the atomic nucleus. Atomic nuclei consisting of such a magic number of nucleons have a higher average binding energy per nucleon than one would expect based upon predictions such as the mass formula of von Weizsaecker (also called the semi-empirical mass formula – SEMF) and are hence more stable against nuclear decay. Magic numbers are predicted by the nuclear shell model. They are proved by observations showing that there are sudden discontinuities in the proton and neutron separation energies at specific values of Z and N. These correspond to the closing of shells (or sub-shells). Nuclei with closed shells are more tightly bound than the next higher number. The closing of shells occurs at Z or N = 2, 8, 20, 28, (40), 50, 82, 126. It is found that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. Nuclei that have both neutron numbers and proton numbers equal to one of the magic numbers can be called “doubly magic” and are found to be particularly stable.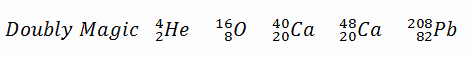
There are further special properties of nuclei, which have a magic number of nucleons:
- Higher abundance in nature. For example, helium-4 is among the most abundant (and stable) nuclei in the universe.
- At the end of the decay series, the stable elements all have a “magic number” of neutrons or protons. The nuclei He-4, O-16, and Pb-208 (82 protons and 126 neutrons) that contain magic numbers of both neutrons and protons are particularly stable. The relative stability of these nuclei is reminiscent of that of inert gas atoms (closed electron shells).
- Nuclei with N = magic number have lower neutron absorption cross-sections than surrounding isotopes.
- These nuclei appear perfectly spherical; they have zero quadrupole electric moments.
- Magic number nuclei have higher first excitation energy.