In physics, the atomic nucleus is the central part of an atom. In comparison to an atom, it is much smaller and contains most of the mass of the atom. Atomic nuclei are not elementary particles, and they are themselves composed of more fundamental particles. The particles that comprise atomic nuclei are termed nucleons, and a nucleon is either a proton or a neutron. Neutrons and protons, i.e., nucleons, are bound together in the atomic nucleus, where they account for 99.9 percent of the atom’s mass. Research in high-energy particle physics in the 20th century revealed that neither the neutron nor the proton is not the smallest building block of matter.
See also: What is Proton
See also: What is Neutron
Protons and neutrons also have their structure. Inside the protons and neutrons, we find true elementary particles called quarks. The proton and neutron are both baryons and both fermions. The proton carries a positive net charge, and the neutron carries a zero net charge. Thus, they can be viewed as two states of the same nucleon. Modern understanding defines isospin as a quantum number related to the strong force distinguishing between these nucleons. The observations have shown that the strong interaction does not distinguish between these nucleons. The strong interaction between any pair of nucleons is the same, independent of whether they are interacting as neutrons or as protons. Instead of regarding protons and neutrons as totally different species, as far as strong interactions are concerned, they are regarded as different isospin states of the same underlying nucleon particle.
The proton has isotopic spin ½ as the neutron has isotopic spin ½, but in the case of the proton, the spin is pointing upwards, and the spin of the neutron is pointing downwards.
Protons and neutrons are bound together within the nucleus through the residual strong force. This fundamental interaction governs the behavior of the quarks that make up the individual protons and neutrons. The residual strong force, also known as the nuclear force, holds neutrons and protons together in nuclei. In nuclei, this force acts against the enormous repulsive electromagnetic force of the protons. The term residual is associated with the fact that it is the residuum of the fundamental strong interaction between the quarks that make up the protons and neutrons. The strong interaction is a very complicated interaction because it significantly varies with distance. At distances comparable to the diameter of a proton, the strong force is approximately 100 times as strong as the electromagnetic force. However, the strong force between quarks becomes weaker at smaller distances, and the quarks begin to behave like independent particles. In particle physics, this effect is known as asymptotic freedom.
Nucleon Number
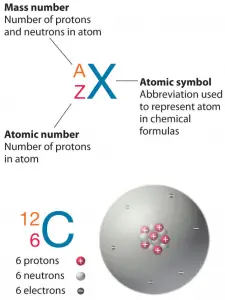The total number of protons and neutrons in the nucleus of an atom is called the atomic mass number (also called nucleon number) of the atom and is given the symbol A. Neutron number plus atomic number equals nucleon number: N+Z=A. The difference between the neutron number and the atomic number is known as the neutron excess: D = N – Z = A – 2Z.
Atomic mass number (nucleon number) determines especially the atomic mass of atoms. The nucleon number is different for each different isotope of a chemical element. The nucleon number is written either after the element name or as a superscript to the left of an element’s symbol. For example, the most common isotope of carbon is carbon-12 or 12C. Note that the unit of measure for mass is the atomic mass unit (amu). One atomic mass unit is equal to 1.66 x 10-24 grams.
Besides the standard kilogram, it is a second mass standard. It is the carbon-12 atom, which, by international agreement, has been assigned a mass of 12 atomic mass units (u). The relation between the two units is one atomic mass unit is equal:
1u = 1.66 x 10-24 grams.
One unified atomic mass unit is approximately the mass of one nucleon (either a single proton or neutron) and is numerically equivalent to 1 g/mol.
For 12C, the atomic mass is exactly 12u since the atomic mass unit is defined from it. The isotopic mass usually differs for other isotopes and is usually within 0.1 u of the mass number. For example, 63Cu (29 protons and 34 neutrons) has a mass number of 63, and an isotopic mass in its nuclear ground state is 62.91367 u.
There are two reasons for the difference between mass number and isotopic mass, known as the mass defect:
- The neutron is slightly heavier than the proton, increasing the mass of nuclei with more neutrons than protons relative to the atomic mass unit scale based on 12C with equal numbers of protons and neutrons.
- The nuclear binding energy varies between nuclei, and a nucleus with greater binding energy has lower total energy and a lower mass according to Einstein’s mass-energy equivalence relation E = mc2. For 63Cu, the atomic mass is less than 63, so this must be the dominant factor.
Note that it was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons, and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=mc2), this binding energy is proportional to this mass difference, known as the mass defect.
Conservation of Nucleon Number in Nuclear Reactions
In general, the nucleon number is not conserved in nuclear reactions.
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for the charge, momentum, angular momentum, and energy (including rest energies). Additional conservation laws not anticipated by classical physics are electric charge, lepton number, and baryon number. Certain of these laws are obeyed under all circumstances, and others are not. We have accepted the conservation of energy and momentum. In reactor physics (non-relativistic physics), we assume that the number of protons (the atomic number), the number of neutrons (the neutron number), and its sum (the nucleon number) are usually separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, we shall find that these principles must be extended when we consider relativistic nuclear energies or those involving weak interactions (e.g., in beta decay, the atomic number is not conserved).
Instead of nucleon number conservation, physicists define the baryon number, which is a conserved quantum number in all particle reactions.
Baryon number is a generalization of nucleon number, which is conserved in non-relativistic nuclear reactions and decays. The law of conservation of baryon number states that:
The sum of the baryon number of all incoming particles is the same as the sum of the baryon numbers of all particles resulting from the reaction.
Number of Nucleons and Nuclear Stability
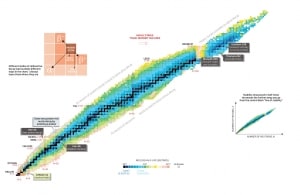
Nuclear stability is a concept that helps identify an isotope’s stability. It is needed to find the ratio of neutrons to protons to identify the stability of an isotope. To determine the stability of an isotope, you can use the ratio neutron/proton (N/Z). Also, to help understand this concept, there is a chart of the nuclides, known as a Segre chart. This chart shows a plot of the known nuclides as a function of their atomic and neutron numbers. It can be observed from the chart that there are more neutrons than protons in nuclides with Z greater than about 20 (Calcium). These extra neutrons are necessary for the stability of the heavier nuclei. The excess neutrons act somewhat like nuclear glue.
See also: Live chart – iaea.org
Detail of Nuclide Chart.
Source: Livechart – IAEA.org
Atomic nuclei consist of protons and neutrons, which attract each other through the nuclear force, while protons repel each other via the electric force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons which form stable nuclei.
Neutrons stabilize the nucleus because they attract each other and protons, which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many or too few neutrons for a given number of protons, the resulting nucleus is not stable and undergoes radioactive decay. Unstable isotopes decay through various radioactive decay pathways, most commonly alpha decay, beta decay, or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission, are known. It should be noted that all of these decay pathways may be accompanied by the subsequent emission of gamma radiation. Pure alpha or beta decays are very rare.
See also: Pauli Exclusion Principle
See also: Unstable Nuclei
Magic Numbers of Nucleons
A magic number is a number of nucleons in a nucleus, corresponding to complete shells within the atomic nucleus. Atomic nuclei consisting of such a magic number of nucleons have a higher average binding energy per nucleon than one would expect based upon predictions such as the mass formula of von Weizsaecker (also called the semi-empirical mass formula – SEMF) and are hence more stable against nuclear decay. Magic numbers are predicted by the nuclear shell model. They are proved by observations showing that there are sudden discontinuities in the proton and neutron separation energies at specific values of Z and N. These correspond to the closing of shells (or sub-shells). Nuclei with closed shells are more tightly bound than the next higher number. The closing of shells occurs at Z or N = 2, 8, 20, 28, (40), 50, 82, 126. It is found that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. Nuclei that have both neutron numbers and proton numbers equal to one of the magic numbers can be called “doubly magic” and are found to be particularly stable.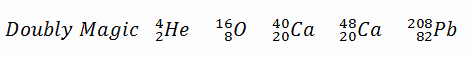
There are further special properties of nuclei, which have a magic number of nucleons:
- Higher abundance in nature. For example, helium-4 is among the most abundant (and stable) nuclei in the universe.
- At the end of the decay series, the stable elements all have a “magic number” of neutrons or protons. The nuclei He-4, O-16, and Pb-208 (82 protons and 126 neutrons) that contain magic numbers of both neutrons and protons are particularly stable. The relative stability of these nuclei is reminiscent of that of inert gas atoms (closed electron shells).
- Nuclei with N = magic number have lower neutron absorption cross-sections than surrounding isotopes.
- These nuclei appear perfectly spherical in shape; they have zero quadrupole electric moments.
- Magic number nuclei have higher first excitation energy.