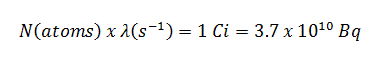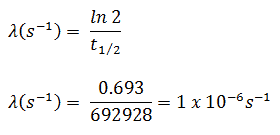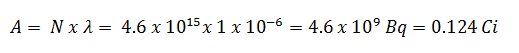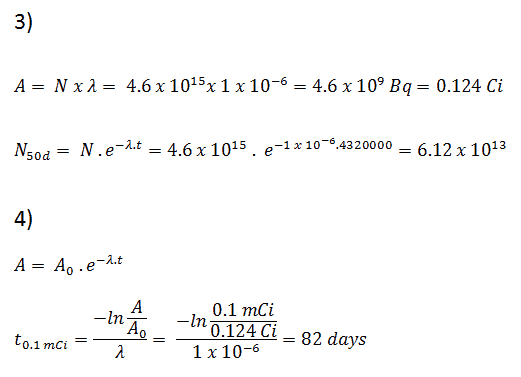In nuclear physics and chemistry, the various species of atoms whose nuclei contain particular numbers of protons and neutrons are called nuclides. Nuclides are also characterized by their nuclear energy states (e.g., metastable nuclide 242mAm). Each nuclide is denoted by the chemical symbol of the element (this specifies Z) with the atomic mass number as a superscript. Isotopes are nuclides with the same atomic number and are therefore the same element but differ in the number of neutrons.
Some nuclides are unstable and radioactive. These nuclides are known as radionuclides (radioactive nuclides) or radioisotopes (radioactive isotopes). These unstable isotopes decay through various radioactive decay pathways, most commonly alpha decay, beta decay, gamma decay, or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission, are known.
As was written, radioactive decay of radionuclides is a random process at the level of single atoms. According to quantum theory, predicting when a particular atom will decay is impossible. In other words, a nucleus of a radionuclide has no “memory.” A nucleus does not “age” over time. Thus, the probability of its breaking down does not increase with time but stays constant no matter how long the nucleus has existed.
Therefore, the rate of nuclear decay can also be measured in terms of half-lives. Each radionuclide has its particular half-life that never changes, regardless of the quantity or form of the material (i.e., solid, liquid, gas, element, or compound) or its history. If a radioisotope has a half-life of 14 days, half of its atoms will have decayed within 14 days. In 14 more days, half of that remaining half will decay, and so on.
Half-lives range from millionths of a second for highly radioactive fission products to billions of years for long-lived materials (such as naturally occurring uranium). After five half-lives have elapsed, only 1/32, or 3.1%, of the original number of atoms remains. After seven half-lives, only 1/128, or 0.78%, of the atoms remain. The number of atoms existing after 5 to 7 half-lives can usually be assumed to be negligible.
The fraction of the original activity remaining after succeeding half-lives is:
Activity after 1 half-life = ½ of the original
Activity after 2 half-lives = ½ x ½ = ¼ of the original
Activity after 3 half-lives = ½ x ½ x ½ = (½)3 = 1/8 of the original
Activity after 4 half-lives = (½)4 = 1/16 of the original
Activity after 5 half-lives = (½)5 = 1/32 of the original
Activity after 6 half-lives = (½)6 = 1/64 of the original
Activity after 7 half-lives = (½)7 = 1/128 of the original
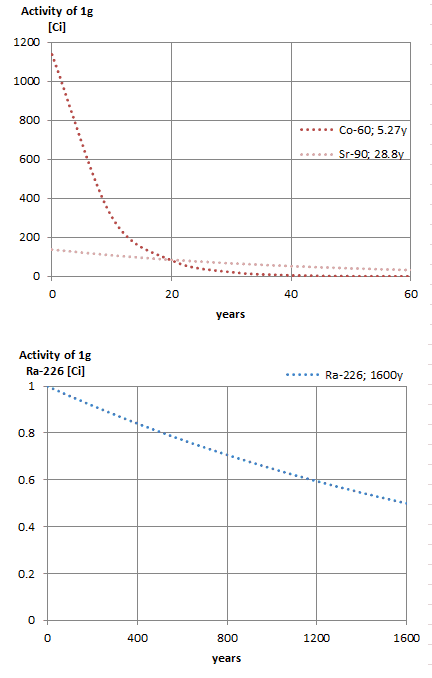Notice that short half-lives go with large decay constants. Radioactive material with a short half-life is much more radioactive (at the time of production) but will lose its radioactivity rapidly. No matter how long or short the half-life is after seven half-lives have passed, there is less than 1 percent of the initial activity remaining.
The radioactive decay law states that the probability per unit time that a nucleus will decay is a constant, independent of time. This constant is called the decay constant and is denoted by λ, “lambda.” This constant probability may vary greatly between different types of nuclei, leading to the many different observed decay rates. The radioactive decay of a certain number of atoms (mass) is exponential in time.
Radioactive decay law: N = N.e-λt
The radioactive decay law can also be derived for activity calculations or mass of radioactive material calculations:
(Number of nuclei) N = N.e-λt (Activity) A = A.e-λt (Mass) m = m.e-λt
where N (number of particles) is the total number of particles in the sample, A (total activity) is the number of decays per unit time of a radioactive sample, and m is the mass of remaining radioactive material.
Half-Life and Radioactivity of Radionuclides
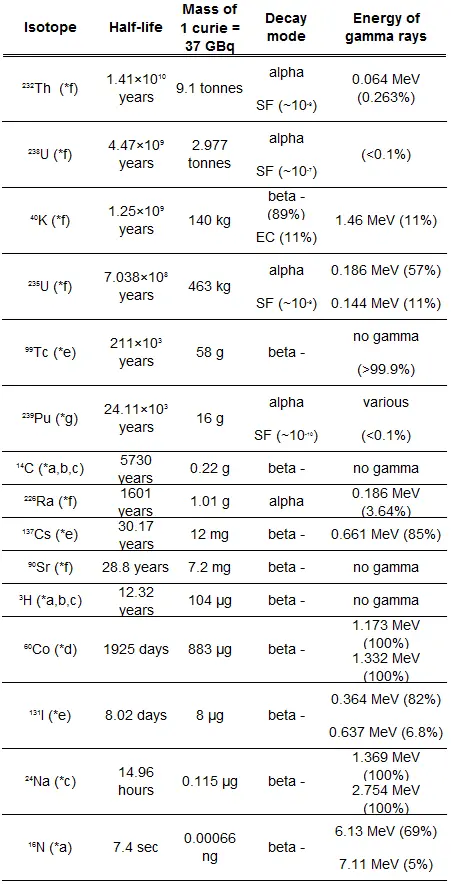
The relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown in the figure. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
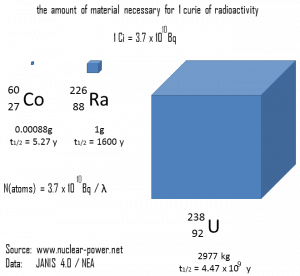The following figure illustrates the amount of material necessary for 1 curie of radioactivity. Obviously, the longer the half-life, the greater the quantity of radionuclide needed to produce the same activity. Of course, the longer-lived substance will remain radioactive for much longer. As can be seen, the amount of material necessary for 1 curie of radioactivity can vary from an amount too small to be seen (0.00088 gram of cobalt-60), through 1 gram of radium-226, to almost three tons of uranium-238.
Example – Radioactivity of Radionuclide
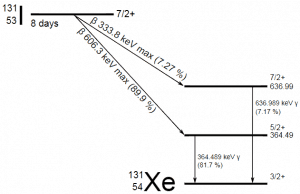A sample of material contains 1 microgram of iodine-131. Note that iodine-131 plays a major role as a radioactive isotope present in nuclear fission products. It is a major contributor to health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.
Calculate:
- The number of iodine-131 atoms is initially present.
- The activity of the iodine-131 in curies.
- The number of iodine-131 atoms will remain in 50 days.
- The time it will take for the activity to reach 0.1 mCi.
Solution:
- The number of atoms of iodine-131 can be determined using isotopic mass as below.
NI-131 = mI-131 . NA / MI-131
NI-131 = (1 μg) x (6.02×1023 nuclei/mol) / (130.91 g/mol)
NI-131 = 4.6 x 1015 nuclei
- The activity of the iodine-131 in curies can be determined using its decay constant:
The iodine-131 has a half-life of 8.02 days (692928 sec), and therefore its decay constant is:
Using this value for the decay constant, we can determine the activity of the sample:
3) and 4) The number of iodine-131 atoms that will remain in 50 days (N50d) and the time it will take for the activity to reach 0.1 mCi can be calculated using the decay law:
As can be seen, after 50 days, the number of iodine-131 atoms and thus the activity will be about 75 times lower. After 82 days, the activity will be approximately 1200 times lower. Therefore, the time of ten half-lives (factor 210 = 1024) is widely used to define residual activity.
