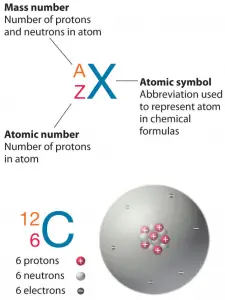
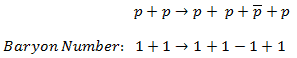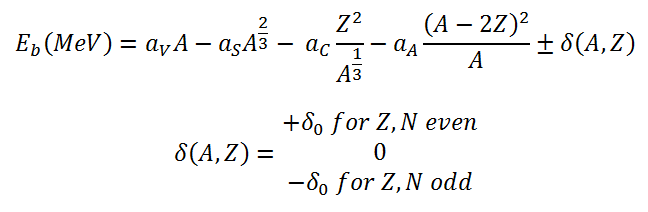The atom consists of a small but massive nucleus surrounded by a cloud of rapidly moving electrons. The nucleus is composed of protons and neutrons. The total number of protons and neutrons in the nucleus of an atom is called the atomic mass number (or the mass number) of the atom and is given the symbol A.
Neutron number plus atomic number equal atomic mass number: N+Z=A. The difference between the neutron number and the atomic number is known as the neutron excess: D = N – Z = A – 2Z.
The atom’s chemical properties are determined by the number of protons and the number and arrangement of electrons. The configuration of these electrons follows the principles of quantum mechanics. The number of electrons in each element’s electron shells, particularly the outermost valence shell, is the primary factor determining its chemical bonding behavior. In the periodic table, the elements are listed to increase the atomic number Z.
The nuclear properties (atomic mass, nuclear cross-sections) of the element are determined by the number of protons (atomic number) and the number of neutrons (neutron number). For example, actinides with odd neutron numbers are usually fissile (fissionable with slow neutrons), while actinides with even neutron numbers are not fissile (but fissionable with fast neutrons). Due to the Pauli exclusion principle, heavy nuclei with an even number of protons and an even number of neutrons are (due to the Pauli exclusion principle) very stable thanks to the occurrence of ‘paired spin.’ On the other hand, nuclei with an odd number of protons and neutrons are mostly unstable.
See also: Weizsaecker Formula Asymmetry and Pairing term
The atomic mass number determines especially the atomic mass of atoms, and the mass number is different for each different isotope of a chemical element.
The mass number is written either after the element name or as a superscript to the left of an element’s symbol. For example, the most common isotope of carbon is carbon-12 or 12C.
Atomic Number, Neutron Number, and Nuclear Stability
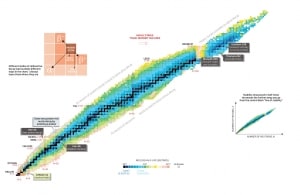
Nuclear stability is a concept that helps identify an isotope’s stability. It is needed to find the ratio of neutrons to protons to identify the stability of an isotope. To determine the stability of an isotope, you can use the ratio neutron/proton (N/Z). Also, to help understand this concept, there is a chart of the nuclides, known as a Segre chart. This chart shows a plot of the known nuclides as a function of their atomic and neutron numbers. It can be observed from the chart that there are more neutrons than protons in nuclides with Z greater than about 20 (Calcium). These extra neutrons are necessary for the stability of the heavier nuclei. The excess neutrons act somewhat like nuclear glue.
See also: Live chart – iaea.org
Atomic nuclei consist of protons and neutrons, which attract each other through the nuclear force, while protons repel each other via the electric force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons, which form stable nuclei.
Neutrons stabilize the nucleus because they attract each other and protons, which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many or too few neutrons for a given number of protons, the resulting nucleus is not stable and undergoes radioactive decay. Unstable isotopes decay through various radioactive decay pathways, most commonly alpha decay, beta decay, or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission, are known. We should note that all of these decay pathways may be accompanied by the subsequent emission of gamma radiation. Pure alpha or beta decays are very rare.
Atomic Mass Number – Does it conserve in a nuclear reaction?
In general, the atomic mass number is not conserved in nuclear reactions.
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for electric charge, momentum, angular momentum, and energy (including rest energies). Other conservation laws not anticipated by classical physics are electric charge, lepton number, and baryon number. Certain of these laws are obeyed under all circumstances; others are not. We have accepted the conservation of energy and momentum. In reactor physics (non-relativistic physics), we assume that the number of protons (the atomic number), the number of neutrons (the neutron number), and its sum (the atomic mass number) are usually separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, where we consider relativistic nuclear energies or those involving weak interactions (e.g., in beta decay, the atomic number is not conserved), we shall find that we must extend these principles.
Instead of mass number conservation, physicists define the baryon number, a conserved quantum number in all particle reactions.
Baryon number is a generalization of nucleon number, which is conserved in non-relativistic nuclear reactions and decays. The law of conservation of baryon number states that:
The sum of the baryon number of all incoming particles is the same as the sum of the baryon numbers of all particles resulting from the reaction.
For example, the following reaction (proton-antiproton pair production) does conserve B and does occur if the incoming proton has sufficient energy (the threshold energy = 5.6 GeV):
As indicated, B = +2 on both sides of this equation.
From these and other reactions, the conservation of the baryon number has been established as a basic principle of physics.
This principle provides the basis for the stability of the proton. Since the proton is the lightest particle among all baryons, the hypothetical products of its decay would have to be non-baryons. Thus, the decay would violate the conservation of the baryon number. It must be added some theories have suggested that protons are, in fact, unstable with a very long half-life (~1030 years) and that they decay into leptons. There is currently no experimental evidence that proton decay occurs.
Atomic Mass Number and Neutron Slowing Down
The moderator, which is important in thermal reactors, is used to moderate, that is, to slow down neutrons from fission to thermal energies. The probability of fission occurring depends on incident neutron energy, and physicists calculate with fission cross-section, which determines this probability.
Nuclei with low mass numbers are most effective for this purpose, so the moderator is always a low-mass-number material. Commonly used moderators include regular (light) water (roughly 75% of the world’s reactors), solid graphite (20% of reactors), and heavy water (5% of reactors). Beryllium and beryllium oxide (BeO) have been used occasionally, but they are very costly. Low-mass number materials are effective due to high logarithmic energy decrement per collision (ξ) as a key material constant describing energy transfers during a neutron slowing down.
Atomic Mass Number and Nuclear Radius
Typical nuclear radii are of the order 10−14 m. Assuming spherical shape, nuclear radii can be calculated according to the following formula:
r = r0 . A1/3
where r0 = 1.2 x 10-15 m = 1.2 fm
If we use this approximation, we, therefore, expect the geometrical cross-sections of nuclei to be of the order of πr2 or 4.5×10−30 m² for hydrogen nuclei or 1.74×10−28 m² for 238U nuclei.
Atomic Mass Number and Nuclear Fission
We can write the nuclear binding energy as a function of the mass number A and the number of protons Z based on the liquid drop model as:
This formula is called the Weizsaecker Formula (or the semi-empirical mass formula). With the aid of the Weizsaecker formula, we can calculate the binding energy very well for nearly all isotopes, and this formula provides a good fit for heavier nuclei.
From the nuclear binding energy curve and the table, it can be seen that, in the case of splitting a 235U nucleus into two parts, the binding energy of the fragments (A ≈ 120) together is larger than that of the original 235U nucleus. According to the Weizsaecker formula, the total energy released for such a reaction will be approximately 235 x (8.5 – 7.6) ≈ 200 MeV.
As well as, the critical energy depends on the nuclear structure and is quite large for light nuclei with Z < 90. For heavier nuclei with Z > 90, the critical energy is about 4 to 6 MeV for A-even nuclei and generally is much lower for A-odd nuclei.
Atomic Mass Number and Atomic Mass (Isotopic Mass)
The size and mass of atoms are so small that standard measuring units, while possible, are often inconvenient. Units of measure have been defined for mass and energy on the atomic
scale to make measurements more convenient to express. The unit of measure for mass is the atomic mass unit (amu). One atomic mass unit is equal to 1.66 x 10-24 grams.
Besides the standard kilogram, it is a second mass standard. It is the carbon-12 atom, which, by international agreement, has been assigned a mass of 12 atomic mass units (u). The relation between the two units is
One atomic mass unit is equal:
1u = 1.66 x 10-24 grams.
One unified atomic mass unit is approximately the mass of one nucleon (either a single proton or neutron) and is numerically equivalent to 1 g/mol.
For 12C, the atomic mass is exactly 12u since the atomic mass unit is defined from it. The isotopic mass usually differs for other isotopes and is usually within 0.1 u of the mass number. For example, 63Cu (29 protons and 34 neutrons) has a mass number of 63, and an isotopic mass in its nuclear ground state is 62.91367 u.
There are two reasons for the difference between mass number and isotopic mass, known as the mass defect:
- The neutron is slightly heavier than the proton, increasing the mass of nuclei with more neutrons than protons relative to the atomic mass unit scale based on 12C with equal numbers of protons and neutrons.
- The nuclear binding energy varies between nuclei, and a nucleus with greater binding energy has lower total energy and a lower mass according to Einstein’s mass-energy equivalence relation E = mc2. For 63Cu, the atomic mass is less than 63, so this must be the dominant factor.
Atomic Mass – Periodic Table
For full interactivity, please visit material-properties.org.