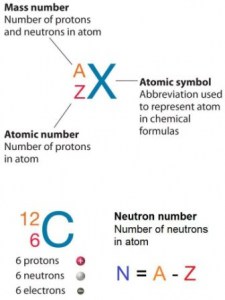
The atom consists of a small but massive nucleus surrounded by a cloud of rapidly moving electrons. The nucleus is composed of protons and neutrons, and the total number of neutrons in the nucleus of an atom is called the neutron number of the atom and is given the symbol N.
Neutron number plus atomic number equal atomic mass number: N+Z=A. The difference between the neutron number and the atomic number is known as the neutron excess: D = N – Z = A – 2Z.
Neutron number is rarely written explicitly in nuclide symbol notation but appears as a subscript to the right of the element symbol. Nuclides with the same neutron number but a different proton number are called isotones.
The atom’s chemical properties are determined by the number of protons and the number and arrangement of electrons. The configuration of these electrons follows the principles of quantum mechanics. The number of electrons in each element’s electron shells, particularly the outermost valence shell, is the primary factor determining its chemical bonding behavior. In the periodic table, the elements are listed to increase the atomic number Z.
The element’s nuclear properties (atomic mass, nuclear cross-sections) are determined by the number of protons and the number of neutrons (neutron number). For example, actinides with odd neutron numbers are usually fissile (fissionable with slow neutrons), while actinides with even neutron numbers are not fissile (but fissionable with fast neutrons). Due to the Pauli exclusion principle, heavy nuclei with an even number of protons and an even number of neutrons are very stable thanks to the occurrence of ‘paired spin’. On the other hand, nuclei with an odd number of protons and neutrons are mostly unstable.
See also: Weizsaecker Formula Asymmetry and Pairing term
Hydrogen (H), for example, consists of one electron and one proton. The number of neutrons in a nucleus is known as the neutron number and is given the symbol N. The total number of nucleons, protons, and neutrons in a nucleus are equal to Z + N = A, where A is called the mass number. The various species of atoms whose nuclei contain particular numbers of protons and neutrons are called nuclides. Each nuclide is denoted by the element’s chemical symbol (this specifies Z) with the atomic mass number as superscript.
Thus the symbol 1H refers to the nuclide of hydrogen with a single proton as a nucleus. 2H is the hydrogen nuclide with a neutron and a proton in the nucleus (2H is also called deuterium or heavy hydrogen). Atoms such as 1H, 2H, whose nuclei contain the same number of protons but the different number of neutrons (different A), are known as isotopes. Hydrogen has identical chemical properties as deuterium but has completely different nuclear properties.
Neutron Number and Nuclear Stability
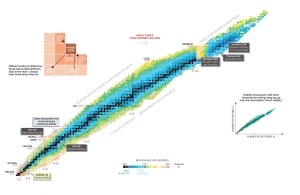
Nuclear Stability is a concept that helps identify an isotope’s stability. It is needed to find the ratio of neutrons to protons to identify the stability of an isotope. To determine the stability of an isotope, you can use the ratio neutron/proton (N/Z). Also, to help understand this concept, there is a chart of the nuclides, known as a Segre chart. This chart shows a plot of the known nuclides as a function of their atomic and neutron numbers. It can be observed from the chart that there are more neutrons than protons in nuclides with Z greater than about 20 (Calcium). These extra neutrons are necessary for the stability of the heavier nuclei. The excess neutrons act somewhat like nuclear glue. Only two stable nuclides have fewer neutrons than protons: hydrogen-1 and helium-3.
See also: Live chart – iaea.org
See also: Weizsaecker Formula Asymmetry and Pairing term
Atomic nuclei consist of protons and neutrons, which attract each other through the nuclear force, while protons repel each other via the electric force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons, which form stable nuclei.
Neutrons stabilize the nucleus because they attract each other and protons, which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many or too few neutrons for a given number of protons, the resulting nucleus is not stable and undergoes radioactive decay. Unstable isotopes decay through various radioactive decay pathways, most commonly alpha decay, beta decay, or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission, are known. It should be noted that all of these decay pathways may be accompanied by the subsequent emission of gamma radiation. Pure alpha or beta decays are very rare.
Neutron Number – Does it conserve in a nuclear reaction?
In general, the neutron number is not conserved in nuclear reactions.
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for the charge, momentum, angular momentum, and energy (including rest energies). Additional conservation laws not anticipated by classical physics are electric charge, lepton number, and baryon number. Certain of these laws are obeyed under all circumstances, and others are not. We have accepted the conservation of energy and momentum. In reactor physics (non-relativistic physics), we assume that the number of neutrons (the neutron number), the number of protons (the proton number), and its sum (the atomic mass number) are usually separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, we shall find that these principles must be extended when we consider relativistic nuclear energies or those involving weak interactions (e.g., in beta decay, the neutron number is not conserved).
