We usually distinguish the binding energy according to these levels:
At the atomic level, the atomic binding energy of the atom derives from the electromagnetic interaction of electrons in the atomic cloud and nucleons (protons) in the nucleus. The atomic binding energy is the energy required to disassemble an atom into free electrons and a nucleus. This is more commonly known as ionization energy.
At the molecular level, the molecular binding energy of the molecule derives from the bond-dissociation energy of atoms in a chemical bond.
At the nuclear level, the nuclear binding energy is the energy required to disassemble (to overcome the strong nuclear force) a nucleus of an atom into its component parts (protons and neutrons).
Nuclear Binding Energy
The component parts of nuclei are neutrons and protons, which are collectively called nucleons. The mass of a nucleus is always less than the sum masses of the constituent protons and neutrons when separated. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=m.c2) this binding energy is proportional to this mass difference, and it is known as the mass defect.
Source: hyperphysics.phy-astr.gsu.edu
During the nuclear splitting or nuclear fusion, some of the mass of the nucleus gets converted into huge amounts of energy. Thus this mass is removed from the total mass of the original particles, and the mass is missing in the resulting nucleus. The nuclear binding energies are enormous. They are on the order of a million times greater than the electron binding energies of atoms.
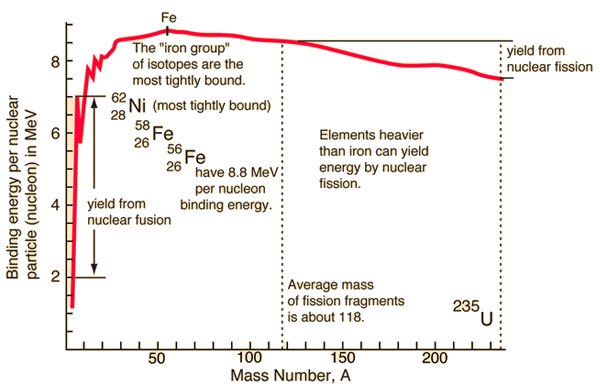
Nuclear Binding Curve
If the splitting releases energy and the fusion release the energy, so where is the breaking point? For understanding this issue, it is better to relate the binding energy to one nucleon to obtain a nuclear binding curve. The binding energy per one nucleon is not linear. There is a peak in the binding energy curve in the region of stability near iron. This means that either the breakup of heavier nuclei than iron or the combining of lighter nuclei than iron will yield energy.
The reason the trend reverses after the iron peak is the growing positive charge of the nuclei. The electric force has a greater range than the strong nuclear force. While the strong nuclear force binds only close neighbors, the electric force of each proton repels the other protons.