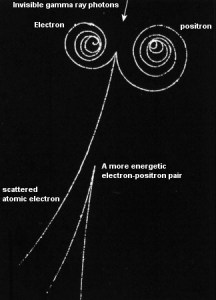
The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with the matter when they are energetic. The track of positrons in a material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.
At the end of their path, positrons differ significantly from electrons. When a positron (antimatter particle) comes to rest, it interacts with an electron (matter particle), resulting in the annihilation of both particles and the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
Positron Annihilation
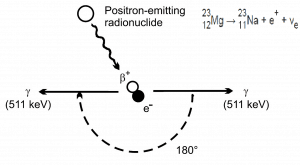
Electron–positron annihilation occurs when a negatively charged electron and a positively charged positron collide. When a low-energy electron annihilates a low-energy positron (the electron’s antiparticle), they can only produce two or more photons (gamma rays). The production of only one photon is forbidden because of the conservation of linear momentum and total energy. The production of another particle is also forbidden because both particles (electron-positron) together do not carry enough mass energy to produce heavier particles. When an electron and a positron collide, they annihilate, resulting in the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
e− + e+ → γ + γ (2x 0.511 MeV)
This process must satisfy several conservation laws, including:
- Conservation of electric charge. The net charge before and after is zero.
- Conservation of linear momentum and total energy. T
- Conservation of angular momentum.
Shielding of Beta Particles – Positrons
Due to the presence of these gamma rays, any positron shield has to include also a gamma-ray shield. A multi-layered radiation shield is appropriate to minimize the bremsstrahlung. Material for the first layer must fulfill the requirements for negative beta radiation shielding. The first layer of such a shield may be a thin aluminium plate (to shield positrons), while the second layer of such a shield may be a dense material such as lead or depleted uranium.
See also: Shielding of Gamma Radiation.
