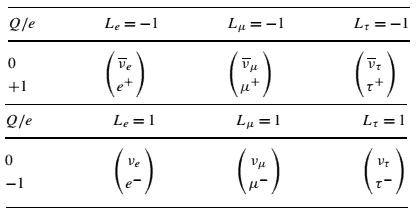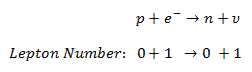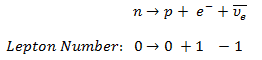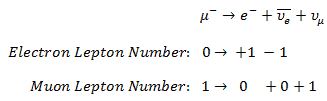In particle physics, the lepton number denotes which particles are leptons and which particles are not. Each lepton has a lepton number of 1, and each antilepton has a lepton number of -1. Other non-leptonic particles have a lepton number of 0. The lepton number is a conserved quantum number in all particle reactions. A slight asymmetry in the laws of physics allowed leptons to be created in the Big Bang.
The conservation of lepton number means that whenever a lepton of a certain generation is created or destroyed in a reaction, a corresponding antilepton from the same generation must be created or destroyed. It must be added, and there is a separate requirement for each of the three generations of leptons, the electron, muon, and tau, and their associated neutrinos.
Example: Electron Capture
Consider the electron capture mode. The reaction involves only first generation leptons: electrons and neutrinos:
The antineutrino cannot be emitted, because in this case the conservation law would not be fulfilled. The particle emitted with the neutron must be a neutrino.
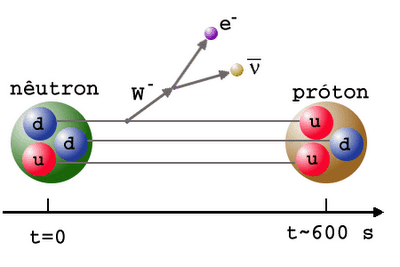
Example: Neutron Decay
Consider the decay of the neutron. The reaction involves only first-generation leptons: electrons and neutrinos:
Since the lepton number must be equal to zero on both sides and it was found that the reaction is a three-particle decay (the electrons emitted in beta decay have a continuous rather than a discrete spectrum), the third particle must be an electron antineutrino.
Source: scienceblogs.com
Example: Muon Decay
The observation of the following decay reaction leads to the conclusion that there is a separate lepton number for muons which must also be conserved.
This is, in fact, the most common decay mode of the –.
