What is Neutron | Definition & Properties

A neutron is one of the subatomic particles that make up matter. The neutron has no electric charge and a rest mass equal to 1.67493 × 10⁻²⁷ kg — marginally greater than that of the proton but nearly 1839 times greater than that of the electron. The neutron has a mean square radius of about 0.8×10−15 m or 0.8 fm, and it is a spin-½ fermion. In the universe, neutrons are abundant, making up more than half of all visible matter.

The quark structure of the neutron. The color assignment of individual quarks is arbitrary, but all three colors must be present. Gluons mediate forces between quarks.
Source: wikipedia.org

The neutrons exist in the nuclei of typical atoms, along with their positively charged counterparts, the protons. Neutrons and protons, commonly called nucleons, are bound together in the atomic nucleus, where they account for 99.9 percent of the atom’s mass. Research in high-energy particle physics in the 20th century revealed that neither the neutron nor the proton is not the smallest building block of matter. Protons and neutrons also have their structure. Inside the protons and neutrons, we find true elementary particles called quarks. Within the nucleus, protons and neutrons are bound together through a strong force. This fundamental interaction governs the behavior of the quarks that make up the individual protons and neutrons.

The competition between two fundamental interactions determines nuclear stability. Protons and neutrons are attracted each other via the strong force. On the other hand, protons repel each other via the electric force due to their positive charge. Therefore neutrons within the nucleus act somewhat like nuclear glue. Neutrons attract each other and protons, which helps offset the electrical repulsion between protons. There are only certain combinations of neutrons and protons, which form stable nuclei. For example, the most common nuclide of the common chemical element lead (Pb) has 82 protons and 126 neutrons.

Nuclear binding energy curve.
Source: hyperphysics.phy-astr.gsu.edu

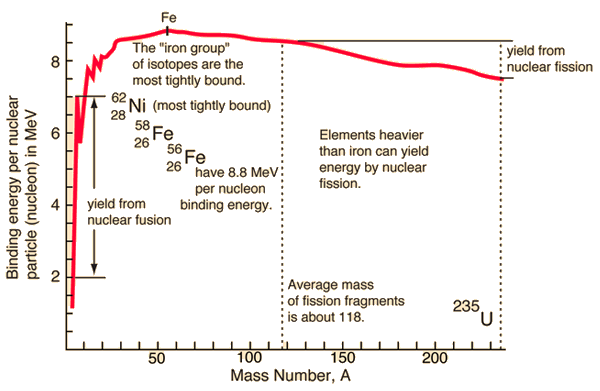
Because of the strength of the nuclear force at short distances, the nuclear binding energy (the energy required to disassemble a nucleus of an atom into its component parts) of nucleons is more than seven orders of magnitude larger than the electromagnetic energy binding electrons in atoms. Therefore, nuclear reactions (such as nuclear fission or nuclear fusion) have an energy density of more than 10 000 000x that of chemical reactions.
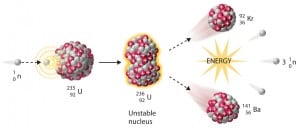
Knowledge of the behavior and properties of neutrons is essential to the production of nuclear power. The neutron was discovered in 1932. The fact that neutrons might act to form a nuclear chain reaction was realized quickly after that. When nuclear fission was discovered in 1938, it became clear that if a fission reaction produced free neutrons, each of these neutrons might cause further fission reaction in a cascade known as a chain reaction. Knowledge of cross-sections (the key parameter representing the probability of interaction between a neutron and a nucleus) became crucial for designing reactor cores and the first nuclear weapon (Trinity, 1945).

Discovery of the Neutron

The story of the discovery of the neutron and its properties is central to the extraordinary developments in atomic physics that occurred in the first half of the 20th century. The neutron was discovered in 1932 by the English physicist James Chadwick. Still, since the time of Ernest Rutherford, it has been known that the atomic mass number A of nuclei is a bit more than twice the atomic number Z for most atoms. Essentially, all the mass of the atom is concentrated in the relatively tiny nucleus. Rutherford’s model for the atom in 1911 claims that atoms have their mass and positive charge concentrated in a very small nucleus.

Chadwicks chamber. — Chadwick’s neutron chamber contains parallel disks of radioactive polonium and beryllium. Radiation is emitted from an aluminum window at the chamber’s end.
Source: imgkid.com

An experimental breakthrough came in 1930 with the observation by Bothe and Becker. They found that unusually penetrating radiation was produced if the very energetic alpha particles emitted from polonium fell on certain light elements, specifically beryllium, boron, or lithium. Since this radiation was not influenced by an electric field (neutrons have no charge), they presumed it was gamma rays (but much more penetrating). It was shown (Curie and Joliot) that when a paraffin target with this radiation is bombarded, it ejected protons with an energy of about 5.3 MeV. Paraffin is high in hydrogen content, hence offers a target dense with protons (since neutrons and protons have almost equal mass, protons scatter energetically from neutrons). These experimental results were difficult to interpret. James Chadwick proved that the neutral particle could not be a photon by bombarding targets other than hydrogen, including nitrogen, oxygen, helium, and argon. Not only were these inconsistent with photon emission on energy grounds, but the cross-section for the interactions was also orders of magnitude greater than that for Compton scattering by photons. In Rome, the young physicist Ettore Majorana suggested that the new radiation interacted with protons required a new neutral particle.

The task was that of determining the mass of this neutral particle. James Chadwick chose to bombard boron with alpha particles and analyze the interaction of the neutral particles with nitrogen. These particular targets were partly chosen because the masses of boron and nitrogen were well known. Using kinematics, Chadwick was able to determine the velocity of the protons. Then through conservation of momentum techniques, he was able to determine that the mass of the neutral radiation was almost the same as that of a proton. In 1932, Chadwick proposed that the neutral particle was Rutherford’s neutron. In 1935, he was awarded the Nobel Prize for his discovery.

Structure of the Neutron

Neutrons and protons are classified as hadrons, subatomic particles subject to the strong force, and baryons since they are composed of three quarks. The neutron is a composite particle made of two down quarks with charge −⅓ e and one up quark with charge +⅔ e. Since the neutron has no net electric charge, it is not affected by electric forces, but the neutron does have a slight distribution of electric charge within it. This results in a non-zero magnetic moment (dipole moment) of the neutron. Therefore the neutron also interacts via electromagnetic interaction but is much weaker than the proton.

The mass of the neutron is 939.565 MeV/c², whereas the mass of the three quarks is only about 12 MeV/c² (only about 1% of the mass-energy of the neutron). Like the proton, most of the mass (energy) of the neutron is in the form of the strong nuclear force energy (gluons). The quarks of the neutron are held together by gluons, the exchange particles for the strong nuclear force. Gluons carry the color charge of the strong nuclear force.

Properties of the Neutron

Key properties of neutrons are summarized below:

Mean square radius of a neutron is ~ 0.8 x 10^-15m (0.8 fermi)
The mass of the neutron is 939.565 MeV/c²
Neutrons are ½ spin particles – fermionic statistics
Neutrons are neutral particles – no net electric charge.
Neutrons have a non-zero magnetic moment.
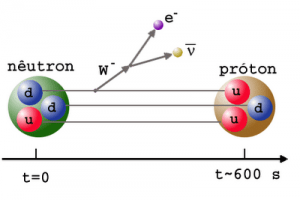
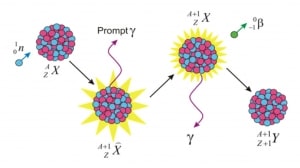
Free neutrons (outside a nucleus) are unstable and decay via beta decay. The decay of the neutron involves the weak interaction and is associated with a quark transformation (a down quark is converted to an up quark).
The mean lifetime of a free neutron is 882 seconds (i.e., the half-life is 611 seconds ).
A natural neutron background of free neutrons exists everywhere on Earth. It is caused by muons produced in the atmosphere, where high-energy cosmic rays collide with particles of Earth’s atmosphere.
Neutrons cannot directly cause ionization. Neutrons ionize matter only indirectly.
Neutrons can travel hundreds of feet in the air without any interaction. Neutron radiation is highly penetrating.
Neutrons trigger nuclear fission.
The fission process produces free neutrons (2 or 3).
Thermal or cold neutrons have wavelengths similar to atomic spacings. They can be used in neutron diffraction experiments to determine the atomic and/or magnetic structure of a material.

Classification of free neutrons according to kinetic energies

Cold Neutrons (0 eV; 0.025 eV). Neutrons in thermal equilibrium with very cold surroundings such as liquid deuterium. This spectrum is used for neutron scattering experiments.
Thermal Neutrons. Neutrons in thermal equilibrium with a surrounding medium. Most probable energy at 20°C (68°F) for Maxwellian distribution is 0.025 eV (~2 km/s). This part of the neutron’s energy spectrum constitutes the most important part of the spectrum in thermal reactors.
Epithermal Neutrons (0.025 eV; 0.4 eV). Neutrons of kinetic energy are greater than thermal. Some reactor designs operate with an epithermal neutron spectrum. This design allows reaching a higher fuel breeding ratio than in thermal reactors.
Neutrons of kinetic energy below the cadmium cut-off energy (~0.5 eV) are strongly absorbed by 113-Cd.
Source: JANIS (Java-based nuclear information software) www.oecd-nea.org/janis/

Cadmium Neutrons (0.4 eV; 0.5 eV). Neutrons of kinetic energy below the cadmium cut-off energy. One cadmium isotope, ¹¹³Cd, absorbs neutrons strongly only if they are below ~0.5 eV (cadmium cut-off energy).
Epicadmium Neutrons (0.5 eV; 1 eV). Neutrons of kinetic energy above the cadmium cut-off energy. These neutrons are not absorbed by cadmium.
Slow Neutrons (1 eV; 10 eV).
Resonance Neutrons (10 eV; 300 eV). The resonance neutrons are called resonance for their special behavior. At resonance energies, the cross-sections can reach peaks more than 100x higher than the base value of the cross-section. At these energies, the neutron capture significantly exceeds the probability of fission. Therefore, it is very important (for thermal reactors) to quickly overcome this range of energy and operate the reactor with thermal neutrons, resulting in an increase in the probability of fission.
Intermediate Neutrons (300 eV; 1 MeV).
Fast Neutrons (1 MeV; 20 MeV). Neutrons of kinetic energy greater than 1 MeV (~15 000 km/s) are usually named fission neutrons. These neutrons are produced by nuclear processes such as nuclear fission or (ɑ,n) reactions. The fission neutrons have a Maxwell-Boltzmann energy distribution with mean energy (for ²³⁵U fission) of 2 MeV. Inside a nuclear reactor, the fast neutrons are slowed down to thermal energies via a process called neutron moderation.
Relativistic Neutrons (20 MeV; ->)

Neutron energies in thermal reactor — Distribution of kinetic energies of neutrons in the thermal reactor. The fission neutrons (fast-flux) are immediately slowed down to the thermal energies via a process called neutron moderation.
Source: serc.carleton.edu

The reactor physics does not need this fine division of neutron energies. The neutrons can be roughly (for purposes of reactor physics) divided into three energy ranges:

Thermal neutrons (0.025 eV – 1 eV).
Resonance neutrons (1 eV – 1 keV).
Fast neutrons (1 keV – 10 MeV).

Even most reactor computing codes use only two neutron energy groups:

Slow neutrons group (0.025 eV – 1 keV).
Fast neutrons group (1 keV – 10 MeV).

Interactions of Neutrons with Matter

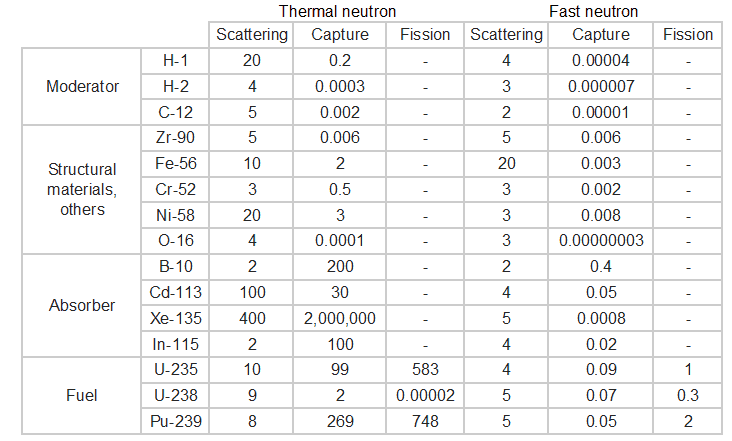
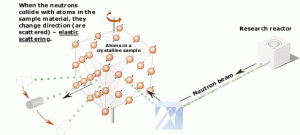
Neutrons are neutral particles. Therefore they travel in straight lines, deviating from their path only when they collide with a nucleus to be scattered into a new direction or absorbed. Neither the electrons surrounding (atomic electron cloud) a nucleus nor the electric field caused by a positively charged nucleus affect a neutron’s flight. In short, neutrons collide with nuclei, not with atoms. A very descriptive feature of the transmission of neutrons through bulk matter is the mean free path length (λ – lambda), which is the mean distance a neutron travels between interactions. It can be calculated from the following equation:

λ=1/Σ

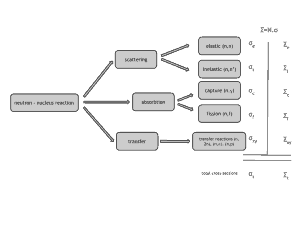
Neutrons may interact with nuclei in one of following ways:

Neutron Cross-section

The extent to which neutrons interact with nuclei is described in terms of quantities known as cross-sections. Cross-sections are used to express the likelihood of particular interaction between an incident neutron and a target nucleus. It must be noted this likelihood does not depend on real target dimensions. In conjunction with the neutron flux, it enables the calculation of the reaction rate, for example, to derive the thermal power of a nuclear power plant. The standard unit for measuring the microscopic cross-section (σ-sigma) is the barn, equal to 10^-28 m². This unit is very small. Therefore barns (abbreviated as “b”) are commonly used. The microscopic cross-section can be interpreted as the effective ‘target area’ that a nucleus interacts with an incident neutron.

A macroscopic cross-section is derived from microscopic and the material density:

Σ=σ.N

Here σ, which has units of m², is referred to as the microscopic cross-section. Since the units of N (nuclei density) are nuclei/m³, the macroscopic cross-section Σ has units of m^-1. This is an incorrect name because it is not a correct unit of cross-sections.

Neutron cross-sections constitute a key parameter of nuclear fuel. Neutron cross-sections must be calculated for new fuel assemblies, usually in two-Dimensional models of the fuel lattice.

The neutron cross-section is variable and depends on:

Target nucleus (hydrogen, boron, uranium, etc.) Each isotope has its own set of cross-sections.
Type of the reaction (capture, fission, etc.). Cross-sections are different for each nuclear reaction.
Neutron energy (thermal neutron, resonance neutron, fast neutron). For a given target and reaction type, the cross-section is strongly dependent on the neutron energy. In the common case, the cross-section is usually much larger at low energies than at high energies. This is why most nuclear reactors use a neutron moderator to reduce the neutron’s energy and thus increase the probability of fission, essential to produce energy and sustain the chain reaction.
Target energy (temperature of target material – Doppler broadening) This dependency is not so significant. Still, the target energy strongly influences the inherent safety of nuclear reactors due to a Doppler broadening of resonances.

Law 1/v

Absorption cross-sections increase for thermal neutrons (in 1/v region) as the neutron’s velocity (kinetic energy) decreases. Therefore the 1/v Law can be used to determine the shift in absorption cross-section if the neutron is in equilibrium with a surrounding medium. This phenomenon is because the nuclear force between the target nucleus and the neutron has a longer time to interact.

$\sigma_a \sim \frac{1}{v}}} \sim \frac{1}{\sqrt{E}}}}} \sim \frac{1}{\sqrt{T}}}}}$

This law is applicable only for absorption cross-section and only in the 1/v region.

Example of cross-sections in 1/v region:

The absorbtion cross-section for 238U at 20°C = 293K (~0.0253 eV) is:

$\sigma_a(293K) = 2.68b$ .

The absorption cross-section for 238U at 1000°C = 1273K is equal to:

This cross-section reduction is caused only due to the shift of temperature of the surrounding medium.

Resonance neutron capture

Resonance peaks for radiative capture of U238. At resonance energies, the probability of capture can be more than 100x higher than the base value.
Source: JANIS program

The absorption cross-section is often highly dependent on neutron energy. Note that nuclear fission produces neutrons with a mean energy of 2 MeV (200 TJ/kg, i.e., 20,000 km/s). The neutron can be roughly divided into three energy ranges:

Fast neutron. (10MeV – 1keV)
Resonance neutron (1keV – 1eV)
Thermal neutron. (1eV – 0.025eV)

The resonance neutrons are called resonance for their special behavior. At resonance energies, the cross-section can reach peaks more than 100x higher as the base value of the cross-section. At these energies, the neutron capture significantly exceeds the probability of fission. Therefore it is very important (for thermal reactors) to quickly overcome this range of energy and operate the reactor with thermal neutrons resulting in an increase in the probability of fission.

Doppler broadening

Doppler effect improves reactor stability. Broadened resonance (heating of a fuel) results in a higher probability of absorption, thus cause negative reactivity insertion (reduction of reactor power).

A Doppler broadening of resonances is a very important phenomenon, which improves reactor stability. The prompt temperature coefficient of most thermal reactors is negative, owing to a nuclear Doppler effect. However, the absorption cross-section depends significantly on incident neutron energy. The shape of the cross-section cur also depends on the target temperature.

Nuclei are located in atoms that are themselves in continual motion owing to their thermal energy. As a result of these thermal motions, neutrons impinging on a target appear to the target’s nuclei to have a continuous spread in energy. This, in turn, affects the observed shape of resonance. The resonance becomes shorter and wider than when the nuclei are at rest.

Although the shape of a resonance changes with temperature, the total area under the resonance remains essentially constant. But this does not imply constant neutron absorption. Despite the constant area under resonance, a resonance integral, which determines the absorption, increases with increasing target temperature. This, of course, decreases coefficient k (negative reactivity is inserted).

Typical cross-sections of materials in the reactor

The following table shows neutron cross-sections of the most common isotopes of the reactor core.

Types of neutron-nuclear reactions

Elastic Scattering Reaction

Generally, a neutron scattering reaction occurs when a target nucleus emits a single neutron after a neutron-nucleus interaction. There is no energy transferred into nuclear excitation in an elastic scattering reaction between a neutron and a target nucleus.

Inelastic Scattering Reaction

In an inelastic scattering reaction between a neutron and a target nucleus, some energy of the incident neutron is absorbed into the recoiling nucleus, and the nucleus remains in the excited state. Thus while momentum is conserved in an inelastic collision, the kinetic energy of the “system” is not conserved.

Neutron Absorption

The neutron absorption reaction is the most important type of reactions that take place in a nuclear reactor. The absorption reactions are reactions where the neutron is completely absorbed, and the compound nucleus is formed. This is a very important feature because the mode of decay of such a compound nucleus does not depend on how the compound nucleus was formed. Therefore a variety of emissions or decays may follow. The most important absorption reactions are divided by the exit channel into two following reactions:

Radiative Capture. Most absorption reactions result in the loss of a neutron coupled with the production of one or more gamma rays. This is referred to as a capture reaction, and it is denoted by σ_γ.

Neutron-induced Fission Reaction. Some nuclei (fissionable nuclei) may undergo a fission event, leading to two or more fission fragments (nuclei of intermediate atomic weight) and a few neutrons. In a fissionable material, the neutron may simply be captured, or it may cause nuclear fission. For fissionable materials, we thus divide the absorption cross-section as σ_a = σ_γ + σ_f.

Radiative Capture

The neutron capture is one of the possible absorption reactions that may occur. In fact, for non-fissionable nuclei, it is the only possible absorption reaction. Capture reactions result in the loss of a neutron coupled with the production of one or more gamma rays. This capture reaction is also referred to as a radiative capture or (n, γ) reaction, and its cross-section is denoted by σ_γ.

The radiative capture is a reaction in which the incident neutron is completely absorbed, and the compound nucleus is formed. The compound nucleus then decays to its ground state by gamma emission. This process can occur at all incident neutron energies, but the probability of the interaction strongly depends on the incident neutron energy and the target energy (temperature). The energy in the center-of-mass system determines this probability.

Nuclear Fission

Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission process often produces free neutrons and photons (in the form of gamma rays) and releases a large amount of energy. In nuclear physics, nuclear fission is either a nuclear reaction or a radioactive decay process. The case of the decay process is called spontaneous fission, and it is a very rare process.

Neutron Emission

Although the neutron emission is usually associated with nuclear decay, it must also be mentioned in connection with neutron nuclear reactions. Some neutrons interact with a target nucleus via a compound nucleus. Among these compound nucleus reactions are reactions in which a neutron is ejected from the nucleus, and they may be referred to as neutron emission reactions. The point is that compound nuclei lose their excitation energy in a way, which is identical to radioactive decay. A very important feature is that the mode of decay of the compound nucleus does not depend on how the compound nucleus was formed.

Charged Particle Ejection

Charged particle reactions are usually associated with the formation of a compound nucleus, which is excited to a high energy level, that such compound nucleus can eject a new charged particle. At the same time, the incident neutron remains in the nucleus. After the new particle is ejected, the remaining nucleus is completely changed but may or may not exist in an excited state depending upon the mass-energy balance of the reaction. This type of reaction is more common for charged particles as incident particles (such as alpha particles, protons, and so on).

The case of neutron-induced charged particle reactions is not so common. Still, some neutron-induced charged particle reactions are important in reactivity control and the detection of neutrons.

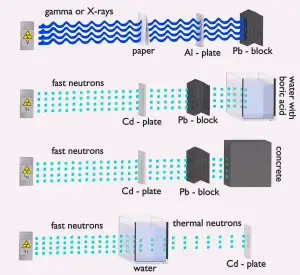
Detection of Neutrons

Since the neutrons are electrically neutral particles, they are mainly subject to strong nuclear forces but not electric forces. Therefore neutrons are not directly ionizing, and they usually have to be converted into charged particles before they can be detected. Generally, every type of neutron detector must be equipped with a converter (to convert neutron radiation to common detectable radiation) and one of the conventional radiation detectors (scintillation detector, gaseous detector, semiconductor detector, etc.).

Neutron converters

Two basic types of neutron interactions with matter are for this purpose available:

Elastic scattering. The free neutron can be scattered by a nucleus, transferring some of its kinetic energy to the nucleus. If the neutron has enough energy to scatter off nuclei, the recoiling nucleus ionizes the material surrounding the converter. Only hydrogen and helium nuclei are light enough for practical application. The conventional detector can collect charges produced in this way to produce a detected signal. Neutrons can transfer more energy to light nuclei. This method is appropriate for detecting fast neutrons (fast neutrons do not have a high cross-section for absorption), allowing the detection of fast neutrons without a moderator.
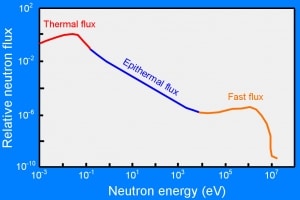
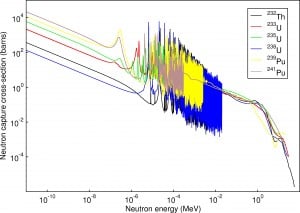
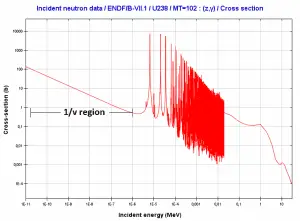
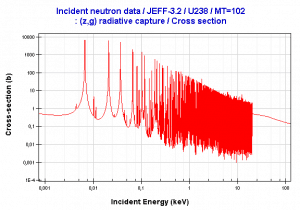
Neutron absorption. This is a common method allowing the detection of neutrons of the entire energy spectrum. This method is based on various absorption reactions (radiative capture, nuclear fission, rearrangement reactions, etc.). The neutron is absorbed by target material (converter), emitting secondary particles such as protons, alpha particles, beta particles, photons (gamma rays), or fission fragments. Some reactions are threshold reactions (requiring minimum energy of neutrons), but most reactions occur at epithermal and thermal energies. That means the moderation of fast neutrons is required leading to poor energy information of the neutrons. The most common nuclei for the neutron converter material are:
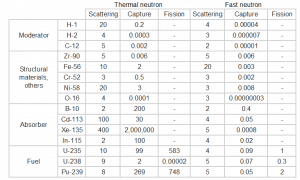
- ¹⁰B(n,α). Where the neutron capture cross-section for thermal neutrons is σ = 3820 barns, and the natural boron has an abundance of ¹⁰B 19,8%.
- ³He(n,p). Where the neutron capture cross-section for thermal neutrons is σ = 5350 barns, and the natural helium has an abundance of ³He 0.014%.
- ⁶Li(n,α). Where the neutron capture cross-section for thermal neutrons is σ = 925 barns, and the natural lithium has an abundance of ⁶Li 7,4%.
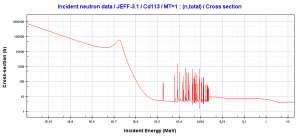
- ¹¹³Cd(n,ɣ). Where the neutron capture cross-section for thermal neutrons is σ = 20820 barns, and the natural cadmium has abundance of ¹¹³Cd 12,2%.
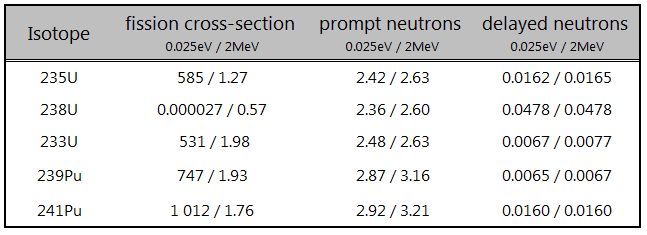
- ²³⁵U(n,fission). Where the fission cross-section for thermal neutrons is σ = 585 barns, and the natural uranium has an abundance of ²³⁵U 0.711%. Uranium as a converter produces fission fragments which are heavy charged particles. This has a significant advantage. The heavy charged particles (fission fragments) create a high output signal because the fragments deposit a large amount of energy in a detector-sensitive volume. This allows easy discrimination of the background radiation (e.i. gamma radiation). This important feature can be used, for example, in a nuclear reactor power measurement, where a significant gamma background accompanies the neutron field.

Shielding of Neutrons

Shielding of Neutron Radiation — Water as a neutron shield

There are three main features of neutrons, which are crucial in the shielding of neutrons.

Neutrons have no net electric charge. Therefore they cannot be affected or stopped by electric forces. Neutrons ionize matter only indirectly, which makes neutrons highly penetrating types of radiation.
Neutrons scatter with heavy nuclei very elastically. Heavy nuclei very hard slow down a neutron, let alone absorb a fast neutron.
An absorption of neutron (one would say shielding) causes the initiation of certain nuclear reactions (e.g.,, radiative capture or even fission), accompanied by a number of other types of radiation. In short, neutrons make matter radioactive. Therefore with neutrons, we have to shield also the other types of radiation.

The best materials for shielding neutrons must be able to:

Slow down neutrons (the same principle as neutron moderation). The first point can be fulfilled only by a material containing light atoms (e.g.,, hydrogen atoms), such as water, polyethylene, and concrete. The nucleus of a hydrogen nucleus contains only a proton. Since a proton and a neutron have almost identical masses, a neutron scattering on a hydrogen nucleus can give up a great amount of its energy (even the entire kinetic energy of a neutron can be transferred to a proton after one collision). This is similar to a billiard. Since a cue ball and another billiard ball have identical masses, the cue ball hitting another ball can be made to stop, and the other ball will start moving with the same velocity. On the other hand, if a ping pong ball is thrown against a bowling ball (neutron vs. heavy nucleus), the ping pong ball will bounce off with very little change in velocity, only a change in direction. Therefore lead is quite ineffective for blocking neutron radiation, as neutrons are uncharged and can simply pass through dense materials.
Table of cross-sections

Absorb this slow neutron. Thermal neutrons can be easily absorbed by capture in materials with high neutron capture cross-sections (thousands of barns) like boron, lithium, or cadmium. Generally, only a thin layer of such absorber is sufficient to shield thermal neutrons. Hydrogen (in the form of water), which can be used to slow down neutrons, has an absorption cross-section of 0.3 barns. This is not enough, but this insufficiency can be offset by sufficient thickness of the water shield.
Shield the accompanying radiation. In the case of cadmium shield, the absorption of neutrons is accompanied by strong emission of gamma rays. Therefore additional shield is necessary to attenuate the gamma rays. This phenomenon practically does not exist for lithium and is much less important for boron as a neutron absorption material. For this reason, materials containing boron are often used in neutron shields. In addition, boron (in the form of boric acid) is well soluble in water, making this combination a very effective neutron shield.

Water as a neutron shield

Water, due to the high hydrogen content and availability, is effective and common neutron shielding. However, due to the low atomic number of hydrogen and oxygen, water is not an acceptable shield against gamma rays. On the other hand, in some cases, this disadvantage (low density) can be compensated by the high thickness of the water shield. In the case of neutrons, water perfectly moderates neutrons, but with the absorption of neutrons by hydrogen nuclei, secondary gamma rays with high energy are produced. These gamma rays highly penetrate matter, and therefore they can increase requirements on the thickness of the water shield. Adding a boric acid can help with this problem (neutron absorption on boron nuclei without strong gamma emission) but results in another problem with corrosion of construction materials.

Concrete as a neutron shield

The most commonly used neutron shielding in many nuclear science and engineering sectors is the shield of concrete. Concrete is also hydrogen-containing material, but unlike water, the concrete has a higher density (suitable for secondary gamma shielding) and does not need any maintenance. Because concrete is a mixture of several different materials, its composition is not constant. So when referring to concrete as a neutron shielding material, the material used in its composition should be told correctly. Generally, concrete is divided into “ordinary” concrete and “heavy” concrete. Heavy concrete uses heavy natural aggregates such as barites (barium sulfate) or magnetite or manufactured aggregates such as iron, steel balls, steel punch, or other additives. As a result of these additives, heavy concrete has a higher density than ordinary concrete (~2300 kg/m³). Very heavy concrete can achieve density up to 5,900 kg/m³ with iron additives or up to 8900 kg/m³ with lead additives. Heavy concrete provides very effective protection against neutrons.

Neutron Sources

A neutron source is any device that emits neutrons. Neutron sources have many applications, and they can be used in research, engineering, medicine, petroleum exploration, biology, chemistry, and nuclear power. A number of factors characterize a neutron source:

Significance of the source
Intensity. The rate of neutrons emitted by the source.
Energy distribution of emitted neutrons.
Angular distribution of emitted neutrons.
Mode of emission. Continuous or pulsed operation.

Classification by significance of the source

Large (Significant) neutron sources
- Nuclear Reactors. There are nuclei that can undergo fission on their own spontaneously, but only certain nuclei, like uranium-235, uranium-233, and plutonium-239, can sustain a fission chain reaction. This is because these nuclei release neutrons when they break apart, which can induce the fission of other nuclei. Uranium-235, which exists as 0.7% of naturally occurring uranium, undergoes nuclear fission with thermal neutrons with the production of, on average, 2.4 fast neutrons and the release of ~ 180 MeV of energy per fission. Free neutrons released by each fission play a very important role as a trigger of the reaction, but they can also be used for another purpose. For example, one neutron is required to trigger further fission. Part of free neutrons (let say 0.5 neutrons/fission) is absorbed in other material, but an excess of neutrons (0.9 neutrons/fission) can leave the surface of the reactor core and can be used as a neutron source.

- Fusion Systems. Nuclear fusion is a nuclear reaction in which two or more atomic nuclei (e.g.,, D+T) collide at very high energy and fuse together. Thy byproduct of DT fusion is a free neutron (see picture). Therefore, nuclear fusion reactions can produce large quantities of neutrons.
- Spallation Sources. A spallation source is a high-flux neutron source in which protons that have been accelerated to high energies hit a heavy target material, causing the emission of neutrons. The reaction occurs above a certain energy threshold for the incident particle, which is typically 5 – 15 MeV.

Medium neutron sources
- Bremssstrahlung from Electron Accelerators / Photofission. When slowed down rapidly in a heavy target, energetic electrons emit intense gamma radiation during the deceleration process. This is known as Bremsstrahlung or braking radiation. The interaction of the gamma radiation with the target produces neutrons via the (γ,n) reaction, or the (γ, fission) reaction when a fissile target is used. e-→Pb → γ→ Pb →(γ,n) and (γ,fission). The Bremsstrahlung γ energy exceeds the binding energy of the “last” neutron in the target. A source strength of 10¹³ neutrons/second produced in short (i.e., < 5 μs) pulses can be readily realized.
- Dense plasma focus. The dense plasma focus (DPF) is a device known as an efficient source of neutrons from fusion reactions. The dense plasma focus (DPF) mechanism is based on nuclear fusion of short-lived plasma of deuterium and/or tritium. This device produces a short-lived plasma by electromagnetic compression and acceleration that is called a pinch. This plasma is during the pinch hot and dense enough to cause nuclear fusion and the emission of neutrons.
- Light ion accelerators. Neutrons can also be produced by particle accelerators using targets of deuterium, tritium, lithium, beryllium, and other low-Z materials. In this case, the target must be bombarded with accelerated hydrogen (H), deuterium (D), or tritium (T) nuclei.

Small neutron sources
- Neutron Generators. Neutrons are produced in the fusion of deuterium and tritium in the following exothermic reaction. ²D + ³T → ⁴He + n + 17.6 MeV. The neutron is produced with a kinetic energy of 14.1 MeV. This can be achieved on a small scale in the laboratory with a modest 100 kV accelerator for deuterium atoms bombarding a tritium target. Continuous neutron sources of ~10¹¹ neutrons/second can be achieved relatively simply.
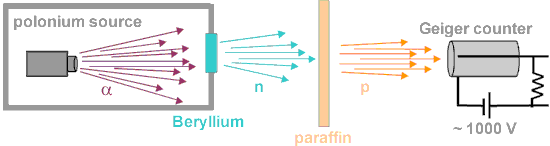
- Radioisotope source – (α,n) reactions. In certain light isotopes, the ‘last’ neutron in the nucleus is weakly bound and is released when the compound nucleus formed following α-particle bombardment decays. The bombardment of beryllium by α-particles leads to the production of neutrons by the following exothermic reaction: ⁴He + ⁹Be→¹²C + n + 5.7 MeV. This reaction yields a weak source of neutrons with an energy spectrum resembling that from a fission source and is used nowadays in portable neutron sources. Radium, plutonium, or americium can be used as an α-emitter.
- Radioisotope source – (γ,n) reactions. (γ,n) reactions can also be used for the same purpose. In this type of source, because of the greater range of the γ-ray, the two physical components of the source can be separated, making it possible to ‘switch off’ the reaction if so required by removing the radioactive source from the beryllium. (γ,n) sources produce monoenergetic neutrons, unlike (α,n) sources. The (γ,n) source uses antimony-124 as the gamma emitter in the following endothermic reaction.

¹²⁴Sb→¹²⁴Te + β− + γ

γ + ⁹Be→⁸Be + n – 1.66 MeV

- Radioisotope source – spontaneous fission. Certain isotopes undergo spontaneous fission with the emission of neutrons. The most commonly used spontaneous fission source is the radioactive isotope californium-252. Cf-252 and other spontaneous fission neutron sources are produced by irradiating uranium or another transuranic element in a nuclear reactor, where neutrons are absorbed in the starting material and its subsequent reaction products, transmuting the starting material into the SF isotope.

See above:

Fundamental Particles

See next:

Alpha Particle