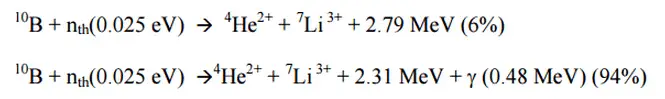Free neutrons can be classified according to their kinetic energy. This energy is usually given in electron volts (eV). The term temperature can also describe this energy representing thermal equilibrium between a neutron and a medium with a certain temperature.
Kinetic Energies of Neutrons – Fast Neutrons
- Cold Neutrons (0 eV; 0.025 eV). Neutrons in thermal equilibrium with very cold surroundings such as liquid deuterium. This spectrum is used for neutron scattering experiments.
- Thermal Neutrons. Neutrons in thermal equilibrium with a surrounding medium. Most probable energy at 20°C (68°F) for Maxwellian distribution is 0.025 eV (~2 km/s). This part of the neutron’s energy spectrum constitutes the most important part of the spectrum in thermal reactors.
- Epithermal Neutrons (0.025 eV; 0.4 eV). Neutrons of kinetic energy are greater than thermal. Some reactor designs operate with an epithermal neutron spectrum. This design allows for a higher fuel breeding ratio than thermal reactors.
-
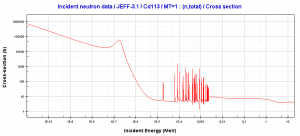
Neutrons of kinetic energy below the cadmium cut-off energy (~0.5 eV) are strongly absorbed by 113-Cd.
Source: JANIS (Java-based nuclear information software) www.oecd-nea.org/janis/Cadmium Neutrons (0.4 eV; 0.5 eV). Neutrons of kinetic energy below the cadmium cut-off energy. One cadmium isotope, 113Cd, absorbs neutrons strongly only if below ~0.5 eV (cadmium cut-off energy).
- Epicadmium Neutrons (0.5 eV; 1 eV). Neutrons of kinetic energy above the cadmium cut-off energy. These neutrons are not absorbed by cadmium.
- Slow Neutrons (1 eV; 10 eV).
- Resonance Neutrons (10 eV; 300 eV). The resonance neutrons are called resonance for their special behavior. At resonance energies, the cross-sections can reach peaks more than 100x higher than the base value of the cross-section. At these energies, the neutron capture significantly exceeds the probability of fission. Therefore it is very important (for thermal reactors) to quickly overcome this range of energy and operate the reactor with thermal neutrons, increasing the probability of fission.
- Intermediate Neutrons (300 eV; 1 MeV).
- Fast Neutrons (1 MeV; 20 MeV). Neutrons of kinetic energy greater than 1 MeV (~15 000 km/s) are usually named fission neutrons. These neutrons are produced by nuclear processes such as nuclear fission or (ɑ,n) reactions. The fission neutrons have a Maxwell-Boltzmann distribution of energy with mean energy (for 235U fission) of 2 MeV. Inside a nuclear reactor, the fast neutrons are slowed down to the thermal energies via a process called neutron moderation.
- Relativistic Neutrons (20 MeV; ->)
The reactor physics does not need this fine division of neutron energies. The neutrons can be roughly (for purposes of reactor physics) divided into three energy ranges:
- Thermal neutrons (0.025 eV – 1 eV).
- Resonance neutrons (1 eV – 1 keV).
- Fast neutrons (1 keV – 10 MeV).
Even most reactor computing codes use only two neutron energy groups:
- Slow neutrons group (0.025 eV – 1 keV).
- Fast neutrons group (1 keV – 10 MeV).
See also: Neutron Energy
Classification of Reactors according to Neutron Flux Spectrum
See also: Neutron Flux Spectra
From the physics point of view, the main differences among reactor types arise from differences in their neutron energy spectra. The basic classification of nuclear reactors is based upon the average energy of the neutrons, which cause the bulk of the fissions in the reactor core. From this point of view, nuclear reactors are divided into two categories:
- Thermal Reactors. Almost all of the current reactors built to date use thermal neutrons to sustain the chain reaction. These reactors contain a neutron moderator that slows neutrons from fission until their kinetic energy is more or less in thermal equilibrium with the atoms (E < 1 eV) in the system.
- Fast Neutron Reactors. Fast reactors contain no neutron moderator and use less-moderating primary coolants because they use fast neutrons (E > 1 keV) to cause fission in their fuel.
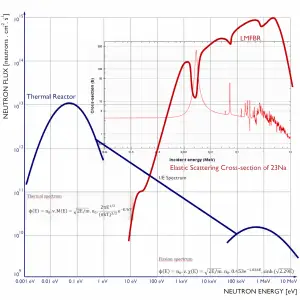
Comparison of neutron spectra in a typical LWR and a sodium-cooled fast breeder reactor. Note that the fast reactor spectrum is highly affected by the elastic scattering cross-section of the used coolant.
Of course, the main differences between these two types are in neutron cross-sections that exhibit significant energy dependency. It can be characterized by the capture-to-fission ratio, which is lower in fast reactors. There is also a difference in the number of neutrons produced per one fission, which is higher in fast reactors than in thermal reactors. These very important differences are caused primarily by differences in neutron fluxes, and therefore it is very important to know detailed neutron energy distribution in a reactor core.
Detection of Neutrons using Ionization Chamber
Since the neutrons are electrically neutral particles, they are mainly subject to strong nuclear forces but not electric ones. Therefore, neutrons are not directly ionizing and usually have to be converted into charged particles before they can be detected. Generally, every type of neutron detector must be equipped with a converter (to convert neutron radiation to common detectable radiation) and one of the conventional radiation detectors (scintillation detector, gaseous detector, semiconductor detector, etc.).
Ionization chambers are often used as the charged particle detection device. For example, if the inner surface of the ionization chamber is coated with a thin coat of boron, the (n, alpha) reaction can occur. Most of (n,alpha) reactions of thermal neutrons are 10B(n,alpha)7Li reactions accompanied by 0.48 MeV gamma emission.
Moreover, isotope boron-10 has a high (n, alpha) reaction cross-section along the entire neutron energy spectrum. The alpha particle causes ionization within the chamber, and ejected electrons cause further secondary ionizations.
Another method for detecting neutrons using an ionization chamber is to use the gas boron trifluoride (BF3) instead of air in the chamber. The incoming neutrons produce alpha particles when reacting with the boron atoms in the detector gas. Either method may be used to detect neutrons in a nuclear reactor. It must be noted that BF3 counters are usually operated in the proportional region.
Detection of Neutrons using Scintillation Counter
Since the neutrons are electrically neutral particles, they are mainly subject to strong nuclear forces but not electric ones. Therefore, neutrons are not directly ionizing and usually have to be converted into charged particles before they can be detected. Generally, every type of neutron detector must be equipped with a converter (to convert neutron radiation to common detectable radiation) and one of the conventional radiation detectors (scintillation detector, gaseous detector, semiconductor detector, etc.). Fast neutrons (>0.5 MeV) primarily rely on the recoil proton in (n,p) reactions. Materials rich in hydrogen, such as plastic scintillators, are best suited for their detection. Thermal neutrons rely on nuclear reactions such as the (n,γ) or (n,α) reactions to produce ionization. Materials such as LiI(Eu) or glass silicates are therefore particularly well-suited for detecting thermal neutrons.