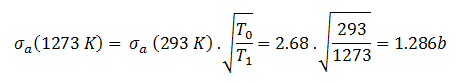Neutrons are neutral particles. Therefore they travel in straight lines, deviating from their path only when they collide with a nucleus to be scattered into a new direction or absorbed. Neither the electrons surrounding (atomic electron cloud) a nucleus nor the electric field caused by a positively charged nucleus affect a neutron’s flight. In short, neutrons collide with nuclei, not with atoms. A very descriptive feature of the transmission of neutrons through bulk matter is the mean free path length (λ – lambda), which is the mean distance a neutron travels between interactions. It can be calculated from the following equation:
λ=1/Σ
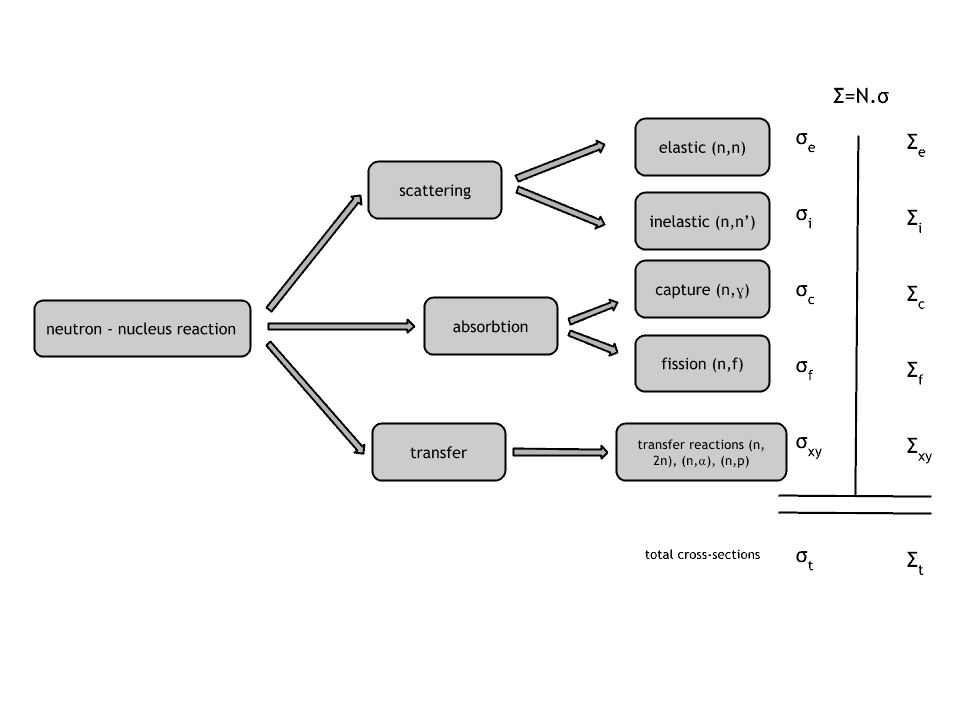
Neutrons may interact with nuclei in one of the following ways:
Types of Interactions of Neutrons with Matter
Neutron cross-section
The extent to which neutrons interact with nuclei is described in terms of quantities known as cross-sections. Cross-sections are used to express the likelihood of particular interaction between an incident neutron and a target nucleus. It must be noted this likelihood does not depend on real target dimensions. In conjunction with the neutron flux, it enables the calculation of the reaction rate, for example, to derive the thermal power of a nuclear power plant. The standard unit for measuring the microscopic cross-section (σ-sigma) is the barn, equal to 10-28 m2. This unit is very small. Therefore barns (abbreviated as “b”) are commonly used. The microscopic cross-section can be interpreted as the effective ‘target area’ that a nucleus interacts with an incident neutron.
A macroscopic cross-section is derived from microscopic and the material density:
Σ=σ.N
Here σ, which has units of m2, is referred to as the microscopic cross-section. Since the units of N (nuclei density) are nuclei/m3, the macroscopic cross-section Σ has units of m-1. Thus, it is an incorrect name because it is not a correct unit of cross-sections.
Neutron cross-sections constitute a key parameter of nuclear fuel. Neutron cross-sections must be calculated for new fuel assemblies, usually in two-Dimensional models of the fuel lattice.
The neutron cross-section is variable and depends on:
- Target nucleus (hydrogen, boron, uranium, etc.) Each isotope has its own set of cross-sections.
- Type of the reaction (capture, fission, etc.). Cross-sections are different for each nuclear reaction.
- Neutron energy (thermal neutron, resonance neutron, fast neutron). For a given target and reaction type, the cross-section is strongly dependent on the neutron energy. In the common case, the cross-section is usually much larger at low energies than at high energies. This is why most nuclear reactors use a neutron moderator to reduce the neutron’s energy and thus increase the probability of fission, essential to produce energy and sustain the chain reaction.
- Target energy (temperature of target material – Doppler broadening) This dependency is not so significant. Still, the target energy strongly influences the inherent safety of nuclear reactors due to a Doppler broadening of resonances.
See also: JANIS (Java-based nuclear information software)
See also: Neutron cross-section
Law 1/v
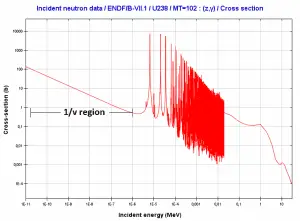
Source: JANIS 4.0
Absorption cross-sections increase for thermal neutrons (in 1/v region) as the neutron’s velocity (kinetic energy) decreases. Therefore the 1/v law can determine a shift in absorption cross-section if the neutron is in equilibrium with a surrounding medium. This phenomenon is because the nuclear force between the target nucleus and the neutron has a longer time to interact.
This law is applicable only for absorption cross-section and only in the 1/v region.
Example of cross-sections in 1/v region:
The absorbtion cross-section for 238U at 20°C = 293K (~0.0253 eV) is:
.
The absorption cross-section for 238U at 1000°C = 1273K is equal to:
This cross-section reduction is caused only due to the shift of temperature of the surrounding medium.
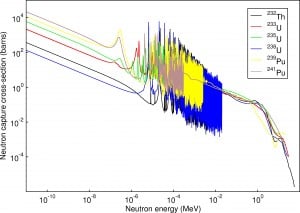
Resonance neutron capture
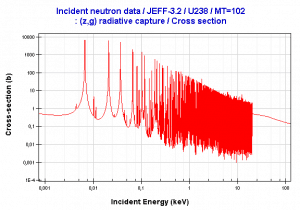
Source: JANIS program
The absorption cross-section is often highly dependent on neutron energy. Note that nuclear fission produces neutrons with a mean energy of 2 MeV (200 TJ/kg, i.e., 20,000 km/s). The neutron can be roughly divided into three energy ranges:
- Fast neutron. (10MeV – 1keV)
- Resonance neutron (1keV – 1eV)
- Thermal neutron. (1eV – 0.025eV)
The resonance neutrons are called resonance for their special behavior. At resonance energies, the cross-section can reach peaks more than 100x higher than the base value of the cross-section. At these energies, the neutron capture significantly exceeds the probability of fission. Therefore it is very important (for thermal reactors) to quickly overcome this range of energy and operate the reactor with thermal neutrons, increasing the probability of fission.
Doppler broadening
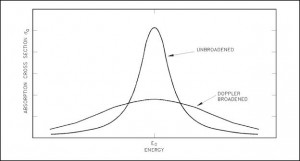
A Doppler broadening of resonances is a very important phenomenon, which improves reactor stability. The prompt temperature coefficient of most thermal reactors is negative, owing to a nuclear Doppler effect. Although the absorption cross-section depends significantly on incident neutron energy, the shape of the cross-section curve also depends on the target temperature.
Nuclei are located in atoms that are themselves in continual motion owing to their thermal energy. As a result of these thermal motions, neutrons impinging on a target appear to the target’s nuclei to have a continuous spread in energy. This, in turn, affects the observed shape of resonance. The resonance becomes shorter and wider than when the nuclei are at rest.
Although the shape of a resonance changes with temperature, the total area under the resonance remains essentially constant. But this does not imply constant neutron absorption. Despite the constant area under resonance, a resonance integral, which determines the absorption, increases with increasing target temperature. This, of course, decreases coefficient k (negative reactivity is inserted).
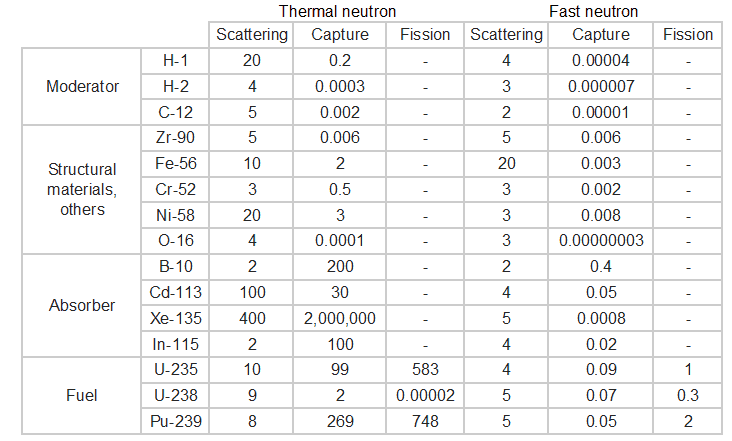
Typical cross-sections of materials in the reactor
The following table shows neutron cross-sections of the most common isotopes of the reactor core.