Facebook Instagram Youtube Twitter

What is Annihilation

Matter – Antimatter Creation and Annihilation

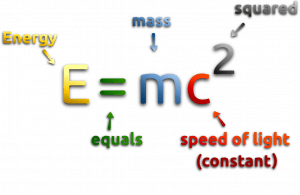E=MC2At the beginning of the 20th century, the notion of mass underwent a radical revision. The mass lost its absoluteness. One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula E = mc2. In other words, energy equals mass multiplied by the speed of light squared.

In the special theory of relativity, certain types of matter may be created or destroyed. Still, the mass and energy associated with such matter remain unchanged in quantity in all of these processes. As a result of the conservation of lepton and baryon numbers,  antimatter (antiparticles) can be created out of energy, but only if a particle counterpart for every antiparticle is created. It will be demonstrated in the following sections.

Matter – Antimatter Annihilation

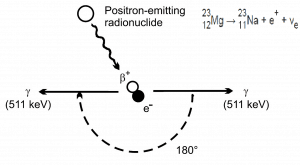
positron annihilation
When a positron (antimatter particle) comes to rest, it interacts with an electron, resulting in the annihilation of both particles and the complete conversion of their rest mass to pure energy in the form of two oppositely directed 0.511 MeV photons.

As was written, a particle and its antiparticle have the same mass as one another but opposite electric charge and other differences in quantum numbers. That means a proton has a positive charge while an antiproton has a negative charge, and therefore they attract each other. A collision between any particle and its antiparticle partner is known to lead to their mutual annihilation. Since matter and antimatter carry an immense amount of energy (due to E = mc2), their mutual annihilation is associated with producing intense photons (gamma rays), neutrinos, and sometimes less-massive particle-antiparticle pairs.

One of the best-known processes is electron-positron annihilation. Electron–positron annihilation occurs when a negatively charged electron and a positively charged positron collide. When a low-energy electron annihilates a low-energy positron (the electron’s antiparticle), it can only produce two or more photons (gamma rays). The production of only one photon is forbidden because of the conservation of linear momentum and total energy. The production of another particle is also forbidden because both particles (electron-positron) together do not carry enough mass energy to produce heavier particles. When an electron and a positron collide, they annihilate, resulting in the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).

e− + e+ → γ + γ (2x 0.511 MeV)

This process must satisfy many conservation laws, including:

  • Conservation of electric charge. The net charge before and after is zero.
  • Conservation of linear momentum and total energy. T
  • Conservation of angular momentum.
 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Antimatter