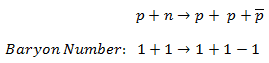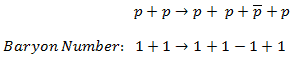The free proton (a proton not bound to nucleons or electrons) is a stable particle that has not been observed to break down spontaneously to other particles. Free protons are found naturally in many situations (e.g., they make up 90% of cosmic rays) in which energies or temperatures are high enough to separate them from electrons, for which they have some affinity.
The decay of proton is also associated with the law of conservation of baryon number. Baryon number is a generalization of nucleon number, conserved in non-relativistic nuclear reactions and decays. The law of conservation of baryon number states that:
The sum of the baryon number of all incoming particles is the same as the sum of the baryon numbers of all particles resulting from the reaction.
For example, the following reaction has never been observed:
even if the incoming proton has sufficient energy and charge energy and is conserved. This reaction does not conserve the baryon number since the left side has B =+2, and the right has B =+1.
On the other hand, the following reaction (proton-antiproton pair production) does conserve B and does occur if the incoming proton has sufficient energy (the threshold energy = 5.6 GeV):
As indicated, B = +2 on both sides of this equation.
From these and other reactions, the conservation of the baryon number has been established as a basic principle of physics. This principle provides the basis for the stability of the proton. Since the proton is the lightest particle among all baryons, the hypothetical products of its decay would have to be non-baryons. Thus, the decay would violate the conservation of the baryon number. It must be added some theories have suggested that protons are, in fact, unstable with a very long half-life (~1030years) and that they decay into leptons. There is currently no experimental evidence that proton decay occurs.