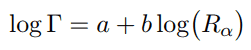Geiger-Nuttall law is a semi-empirical law that expresses the lifetime (half-life) of the alpha emitter in terms of the energy of the released alpha particle. In other words, it states that short-lived isotopes emit more energetic alpha particles than long-lived ones. This rule was formulated by Hans Geiger and John Mitchell Nuttall in 1911, before the development of the theoretical formulation. Geiger-Nuttall law can be mathematically expressed as:
where a and b are empirical constants found from logarithmic plots of experimental data, Rα represents the linear range of alpha particles. Thus it is a direct measure of the kinetic energy of the alpha particle. The width of the resonance (Γ) is generally related to the mean lifetime (τ) of the excited nucleus by the relation: Γ = ℏ / τ
By 1928, George Gamow (and independently by Ronald Gurney and Edward Condon) had solved the theory of alpha decay via quantum tunneling. Using the tunneling mechanism, Gamow, Condon, and Gurney calculated the penetrability of the tunneling α particle through the Coulomb barrier, finding the lifetimes of some α emitting nuclei. The main success of this model was the reproduction of the semi-empirical Geiger-Nuttall law that expresses the lifetimes of the α emitters in terms of the energies of the released α particles.