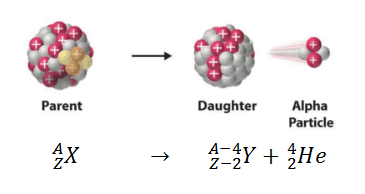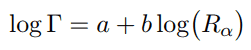Alpha decay (or α-decay and alpha radioactivity) represents the disintegration of a parent nucleus to a daughter through the emission of the nucleus of a helium atom. This transition can be characterized as:
As can be seen from the figure, the alpha particle is emitted in alpha decay.
Among the variety of channels in which a nucleus decays, alpha decay has been one of the most studied. The alpha decay channel in heavy and super heavy nuclei has provided information on the fundamental properties of nuclei far from stability, such as their ground state energies and the structure of their nuclear levels.
Alpha decay is a quantum tunneling process. To be emitted, the alpha particle must penetrate a potential barrier. This is similar to cluster decay, in which an atomic nucleus emits a small “cluster” of neutrons and protons (e.g., 12C).
The height of the Coulomb barrier for nuclei of A « 200 is about 20-25 MeV. The alpha particles emitted in nuclear decay have typical energies of about 5 MeV. On the one hand, an incoming 5 MeV alpha particle is scattered from a heavy nucleus. It cannot penetrate the Coulomb barrier and get sufficiently close to the nucleus to interact via the strong force. On the other hand, a 5 MeV alpha particle bound in a nuclear potential well can tunnel that same Coulomb barrier.
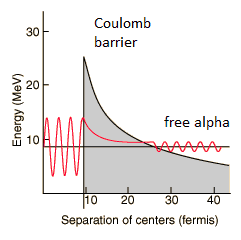 By 1928, George Gamow (and independently by Ronald Gurney and Edward Condon) had solved the theory of alpha decay via quantum tunneling. They assumed that the alpha particle and the daughter nucleus exist within the parent nucleus before its dissociation, namely the decay of quasistationary states (QS). A quasistationary state is defined as a long-lived state that eventually decays. Initially, the alpha cluster oscillates in the potential of the daughter nucleus, with the Coulomb potential preventing their separation. The alpha particle is trapped in a potential well by the nucleus. Classically, it is forbidden to escape, but according to the (then) newly discovered principles of quantum mechanics, it has a tiny (but non-zero) probability of “tunneling” through the barrier and appearing on the other side to escape the nucleus. Using the tunneling mechanism, Gamow, Condon, and Gurney calculated the penetrability of the tunneling α particle through the Coulomb barrier, finding the lifetimes of some α emitting nuclei. The main success of this model was the reproduction of the semi-empirical Geiger-Nuttall law that expresses the lifetimes of the α emitters in terms of the energies of the released α particles. It must be noted that other common forms of decay (e.g., beta decay) are governed by the interplay between nuclear and electromagnetic forces.
By 1928, George Gamow (and independently by Ronald Gurney and Edward Condon) had solved the theory of alpha decay via quantum tunneling. They assumed that the alpha particle and the daughter nucleus exist within the parent nucleus before its dissociation, namely the decay of quasistationary states (QS). A quasistationary state is defined as a long-lived state that eventually decays. Initially, the alpha cluster oscillates in the potential of the daughter nucleus, with the Coulomb potential preventing their separation. The alpha particle is trapped in a potential well by the nucleus. Classically, it is forbidden to escape, but according to the (then) newly discovered principles of quantum mechanics, it has a tiny (but non-zero) probability of “tunneling” through the barrier and appearing on the other side to escape the nucleus. Using the tunneling mechanism, Gamow, Condon, and Gurney calculated the penetrability of the tunneling α particle through the Coulomb barrier, finding the lifetimes of some α emitting nuclei. The main success of this model was the reproduction of the semi-empirical Geiger-Nuttall law that expresses the lifetimes of the α emitters in terms of the energies of the released α particles. It must be noted that other common forms of decay (e.g., beta decay) are governed by the interplay between nuclear and electromagnetic forces.
Special Reference: W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467.
Geiger-Nuttall Law
Geiger-Nuttall law is a semi-empirical law that expresses the lifetime (half-life) of the alpha emitter in terms of the energy of the released alpha particle. In other words, it states that short-lived isotopes emit more energetic alpha particles than long-lived ones. This rule was formulated by Hans Geiger and John Mitchell Nuttall in 1911, before the development of the theoretical formulation. Geiger-Nuttall law can be mathematically expressed as:
where a and b are empirical constants found from logarithmic plots of experimental data, Rα represents the linear range of alpha particles. Thus it is a direct measure of the kinetic energy of the alpha particle. The width of the resonance (Γ) is generally related to the mean lifetime (τ) of the excited nucleus by the relation: Γ = ℏ / τ