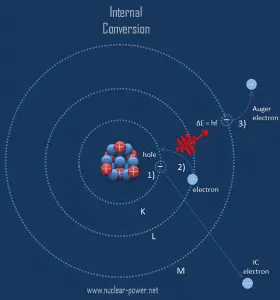
Note that the high-energy electrons resulting from the internal conversion are not called beta particles since the latter come from beta decay, where they are newly created in the nuclear decay process.
As can be seen, if a nucleus decays via internal conversion, atomic and mass numbers of the daughter nucleus remain the same. Still, the daughter nucleus will form a different energy state of the same element. This is very similar to gamma decay, but in this case, no gamma-ray is emitted from an excited nucleus.
Since the process leaves a vacancy in the electron energy level from which the electron came, the outer electrons of the atom cascade down to fill the lower atomic levels, and one or more characteristic X-rays are usually emitted. Sometimes X-ray may interact with another orbital electron, which may be ejected from the atom. This second ejected electron is called an Auger electron. This is very similar to electron capture, but in the case of electron capture, a nucleus changes its atomic number. As a result, the atom thus emits primary high energy electron, characteristic X-rays, or secondary Auger electron, none of which originate in that nucleus.
Theory of Internal Conversion
In the quantum mechanical model of the electron, there is a finite probability of finding the electron within the nucleus. During the internal conversion process, the wavefunction of the K shell electron (inner shell electron) is said to penetrate the volume of the atomic nucleus. Note that typical nuclear radii are of the order of 10-14 m. In this case, the electron may couple to an excited nucleus and take the energy of the nuclear transition directly, without an intermediate gamma-ray. Therefore, most internal conversion electrons (ICE) come from the K shell, as these electrons have the highest probability of being within the nucleus. However, the s states in the L, M, and N shells can also couple to the nuclear fields and cause ICE ejections from those shells.
The internal conversion electron (ICE) energy is the transition energy, Etransition, minus the binding energy of the orbital electron, Eb.e., as:
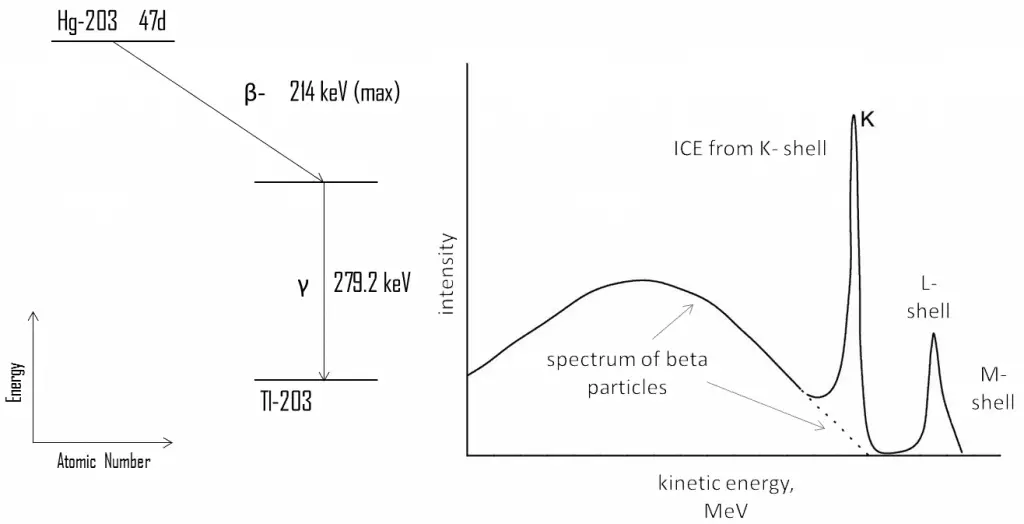
For example, 203Hg is a beta radioactive nuclide, which produces a continuous beta spectrum with maximum energy of 214 keV. This decay produces an excited state of the daughter nucleus 203Tl, which then decays very quickly (~ 10-10 s) to its ground state, emitting a gamma-ray of energy 279.2 keV or an internal conversion electron. If we analyze a spectrum of beta particles, we can see the typical continuous spectrum of beta particles and narrow peaks at specific energies. These peaks are produced by internal conversion electrons (ICE). Since the binding energy of the K electrons in 203Tl amounts to 85.5 keV, the K line has an energy of:
Te (K) = 279.2 – 85.5 = 194 keV
Because of lesser binding energies, the L- and M-lines have higher energies. Since the internal conversion process can interact with any of the orbital electrons, the result is a spectrum of internal conversion electrons, which will be seen as superimposed upon the electron energy spectrum of the beta emission. These relative intensities of these ICE peaks can give information about the electric multipole character of the nucleus and the decay process.
Special reference: Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN 978-0471805533
Internal Conversion Coefficient
The internal conversion coefficient (ICC), α, characterizes the competition between internal conversion and gamma-ray emission. In some cases, internal conversion is favored over gamma decay; in others, it may not be very important. The internal conversion coefficient is defined as the ratio of the number of internal conversions decays to the number of gamma decays. This ICC is defined for each electron shell (i.e., the K, L, and M shells, etc.), such that the total ratio, αtotal, is the sum of the ICCs for each shell as:
αtotal = αK + αL + αM = number of IC / number of gamma decays
For example, in the decay of the excited state at 35 keV of 125Te (which is produced by the decay of 125I), 7% of the decays emit gamma-ray, while 93% emit a conversion electrons. Therefore, an internal conversion coefficient of this excited state (125Te) is ICC = 93/7 = 13.3.
Using the Band-Raman Internal Conversion Coefficient calculator, the ICCs can be calculated using principles of atomic physics since it depends primarily on the density of the atomic electrons at the center of the nucleus. Internal conversion coefficients are observed to increase for increasing atomic number (Z) and decreasing gamma-ray energy.