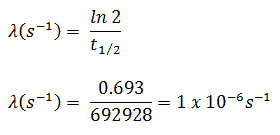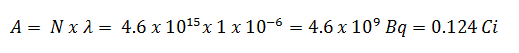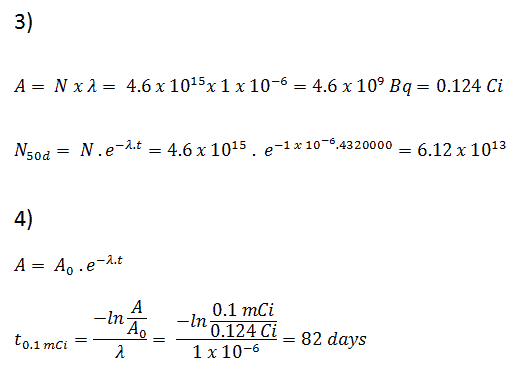The radioactive decay law states that the probability per unit time that a nucleus will decay is a constant, independent of time. This constant is called the decay constant and is denoted by λ, “lambda.”
One of the most useful terms for estimating how quickly a nuclide will decay is the radioactive half-life (t1/2). The half-life is defined as the amount of time it takes for a given isotope to lose half of its radioactivity.
In radioactivity calculations, one of two parameters (decay constant or half-life), which characterize the decay rate, must be known. There is a relation between the half-life (t1/2) and the decay constant λ. The relationship can be derived from the decay law by setting N = ½ No. This gives:
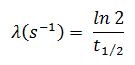 where ln 2 (the natural log of 2) equals 0.693. If the decay constant (λ) is given, it is easy to calculate the half-life, and vice-versa.
where ln 2 (the natural log of 2) equals 0.693. If the decay constant (λ) is given, it is easy to calculate the half-life, and vice-versa.
Example – Radioactive Decay Law
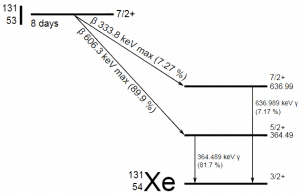 A sample of material contains 1 microgram of iodine-131. Note that iodine-131 plays a major role as a radioactive isotope present in nuclear fission products and is a major contributor to the health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.
A sample of material contains 1 microgram of iodine-131. Note that iodine-131 plays a major role as a radioactive isotope present in nuclear fission products and is a major contributor to the health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.
Calculate:
- The number of iodine-131 atoms is initially present.
- The activity of the iodine-131 in curies.
- The number of iodine-131 atoms will remain in 50 days.
- The time it will take for the activity to reach 0.1 mCi.
Solution:
- The number of atoms of iodine-131 can be determined using isotopic mass as below.
NI-131 = mI-131 . NA / MI-131
NI-131 = (1 μg) x (6.02×1023 nuclei/mol) / (130.91 g/mol)
NI-131 = 4.6 x 1015 nuclei
- The activity of the iodine-131 in curies can be determined using its decay constant:
The iodine-131 has a half-life of 8.02 days (692928 sec), and therefore its decay constant is:
Using this value for the decay constant, we can determine the activity of the sample:
3) and 4) The number of iodine-131 atoms that will remain in 50 days (N50d) and the time it will take for the activity to reach 0.1 mCi can be calculated using the decay law:
As can be seen, after 50 days, the number of iodine-131 atoms and thus the activity will be about 75 times lower. After 82 days, the activity will be approximately 1200 times lower. Therefore, the time of ten half-lives (factor 210 = 1024) is widely used to define residual activity.