Facebook Instagram Youtube Twitter

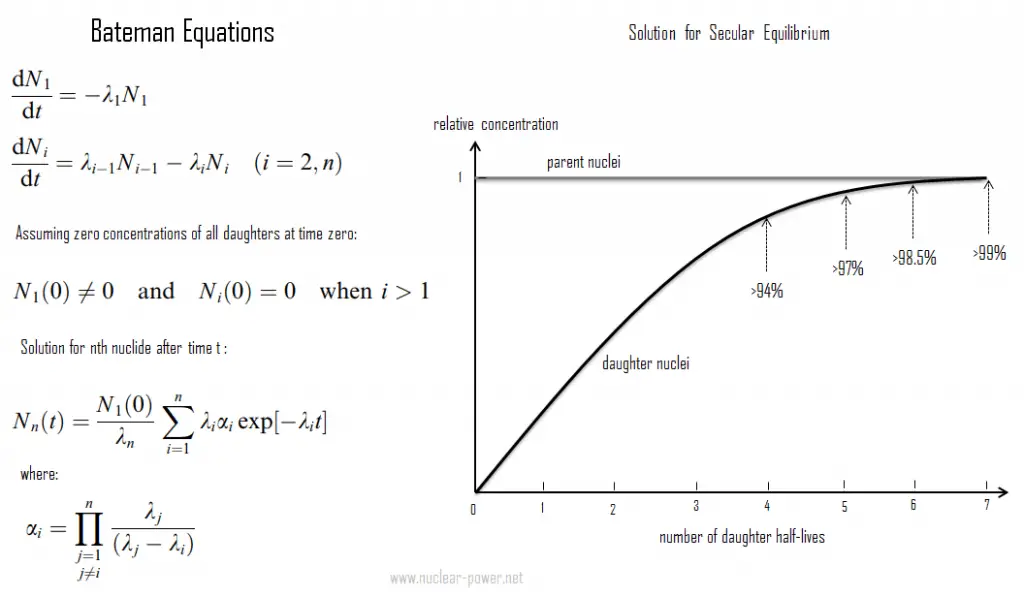
Bateman Equations – Radioactive Decay

In physics, the Bateman equations are a set of first-order differential equations which describe the time evolution of nuclide concentrations undergoing serial or linear decay chain. Ernest Rutherford formulated the model in 1905, and the analytical solution for the case of radioactive decay in a linear chain was provided by Harry Bateman in 1910. This model can also be used in nuclear depletion codes to solve nuclear transmutation and decay problems.

For example, ORIGEN is a computer code system for calculating radioactive materials’ buildup, decay, and processing. ORIGEN uses a matrix exponential method to solve a large system of coupled, linear, first-order ordinary differential equations (similar to the Bateman equations) with constant coefficients.

The Bateman equations for radioactive decay case of n – nuclide series in linear chain describing nuclide concentrations are as follows:

Bateman Equations

Bateman Equations for Nuclear Transmutation

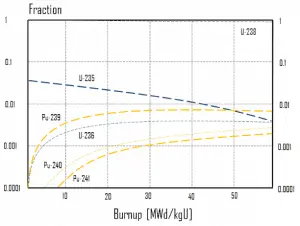
Fuel Depletion - Isotopic Changes
Isotopic changes of 4% uranium-235 fuel as a function of fuel burnup.

As was written, this model can also be used in nuclear depletion codes to solve nuclear transmutation and decay problems. In the case of transmutation, the decay constants that govern Bateman equations for a decay case are substituted by transmutation constants. By the transmutation constant λi,j, we understand the probability of the ith nuclide production per time unit from the jth nuclide destruction as a result of nuclear interaction with the whole spectrum of interacting particles or due to the natural nuclear decay.

These equations are usually used for the exact evolution of isotopic changes in the nuclear fuel during fuel depletion. Fuel depletion is usually modeled mathematically as a set of differential equations known as evolution equations.

Special Reference: Jerzy Cetnar, General solution of Bateman equations for nuclear transmutations. Annals of Nuclear Energy 33 (2006). January 2006.

References:

Radiation Protection:

  1. Knoll, Glenn F., Radiation Detection and Measurement 4th Edition, Wiley, 8/2010. ISBN-13: 978-0470131480.
  2. Stabin, Michael G., Radiation Protection and Dosimetry: An Introduction to Health Physics, Springer, 10/2010. ISBN-13: 978-1441923912.
  3. Martin, James E., Physics for Radiation Protection 3rd Edition, Wiley-VCH, 4/2013. ISBN-13: 978-3527411764.
  4. U.S.NRC, NUCLEAR REACTOR CONCEPTS
  5. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

See above:

Radioactive Equilibrium