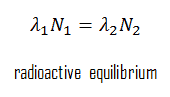In the physics of nuclear decays, a radioactive equilibrium exists when a radioactive nuclide is decaying at the same rate it is being produced. The disintegrating nucleus is usually referred to as the parent nucleus, and the nucleus remains as the daughter nucleus after the event. The daughter nucleus can either be stable or radioactive; if it is radioactive, it decays into a daughter nucleus. Thus, each radioactive parent nucleus can initiate a series of decays, with each decay product having its characteristic decay constant.
The concentration of daughter nuclei in the radioactive equilibrium depends primarily on the proportions of half-lives (or decay constants) of parent and daughter nuclei. Since the production and decay rates are equal, the number of atoms present remains constant over time. In any case, a radioactive equilibrium is not established immediately, but it only takes place after a transition period. This period is the order of a few half-lives of the longest-lived nucleus in the decay chain. In the case of radioactive decay chains, a radioactive equilibrium may be established between each member of the decay chain.
As was written, the proportionality of half-lives is a key parameter that determines the type of radioactive equilibrium:
- Radioactive equilibrium is not established when the half-life of the parent nucleus is shorter than the half-life of the daughter nucleus. In this case, the production rate and decay rate of a certain member of the decay chain cannot be equal.
- Secular radioactive equilibrium exists when the parent nucleus has an extremely long half-life. This type of equilibrium is particularly important in nature. Over the 4.5 billion years of the Earth’s history, especially uranium 238, uranium 235, and thorium 232, members of their decay chains have reached radioactive equilibria between the parent nucleus and the various descendants.
- Transient radioactive equilibrium exists when the half-life of the parent nucleus is longer than the half-life of the daughter nucleus. In this case, the parent nuclide and the daughter nuclide decay at the same rate.
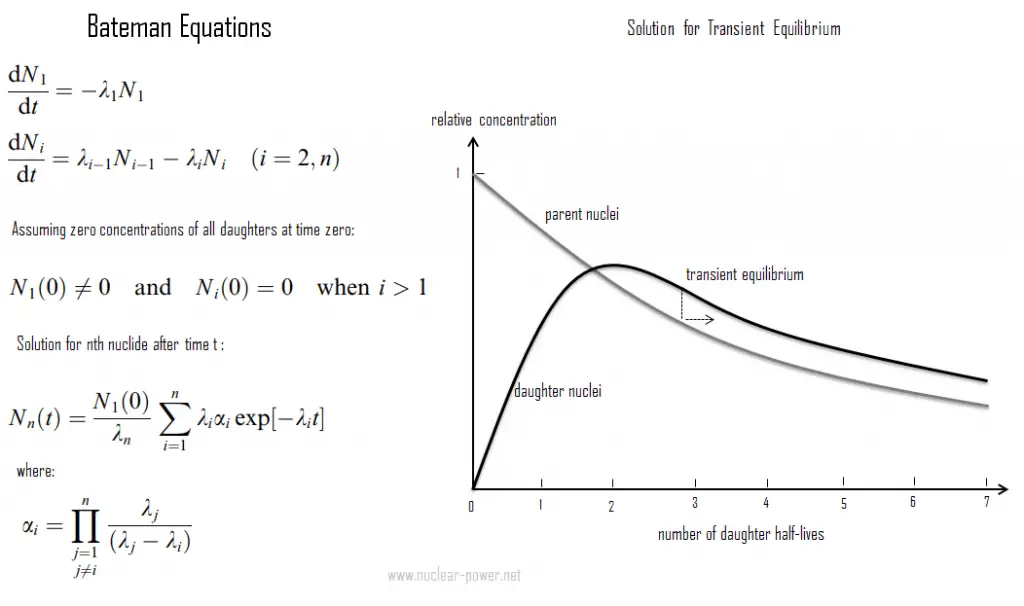
Transient Radioactive Equilibrium
The transient radioactive equilibrium exists when the half-life of the parent nucleus is longer than the half-life of the daughter nucleus. Still, the concentration of parent nuclei significantly decreases in time. In this case, the parent nuclide and the daughter nuclide may decay at essentially the same rate, but both concentrations of nuclides decrease as the concentration of parent nuclei decreases. Contrary to secular equilibrium, the half-life of the daughter nuclei is not negligible compared to the parent’s half-life.
An example of this type of compound decay process is a Technetium-99m generator producing technetium-99m for nuclear medicine diagnostic procedures from molybdenum-99. Technetium-99 m’s short half-life of 6 hours makes storage impossible and would make transport very expensive. Therefore, for medical purposes, molybdenum-99 is used to produce technetium-99m. These two isotopes are in the transient equilibrium. The decay constant for molybdenum-99 is considerably smaller than the decay constant for technetium-99m. Although the decay constant for molybdenum-99 is smaller, the actual decay rate is initially larger than that of molybdenum-99 because of the great difference in their initial concentrations. As the daughter’s concentration increases, the daughter’s decay rate will approach and eventually match the decay rate of the parent. When this occurs, they are said to be in the transient equilibrium. In the case of Technetium-99m generator, transient equilibrium occurs after about four half-lives. Today, technetium-99m is the most utilized element in nuclear medicine and is employed in various nuclear medicine imaging studies.
Also, the transient equilibrium can occasionally be disrupted when one intermediary nucleus leaves the sample where its ancestors are confined.
Transient Radioactive Equilibrium with Source – Example
A special example of radioactive equilibrium is concentrations of iodine-135 and xenon-135 in a nuclear reactor, but in this case, the xenon burnup must be considered. Note that, in this special case, the half-life of the parent nucleus is shorter than the half-life of the daughter nucleus. The production and removal of xenon can be characterized by the following differential equations:
 When the rate of production of iodine equals the rate of removal of iodine, equilibrium exists. This equilibrium is also known as the “xenon 135 reservoir” since all of this iodine must undergo decay to xenon. In equilibrium, the iodine concentration remains constant and is designated NI(eq). The following equation for the iodine equilibrium concentration can be determined from the preceding equation by setting the dNI/dt =0. Since the equilibrium iodine concentration is proportional to the fission reaction rate, it is also proportional to the reactor power level.
When the rate of production of iodine equals the rate of removal of iodine, equilibrium exists. This equilibrium is also known as the “xenon 135 reservoir” since all of this iodine must undergo decay to xenon. In equilibrium, the iodine concentration remains constant and is designated NI(eq). The following equation for the iodine equilibrium concentration can be determined from the preceding equation by setting the dNI/dt =0. Since the equilibrium iodine concentration is proportional to the fission reaction rate, it is also proportional to the reactor power level.
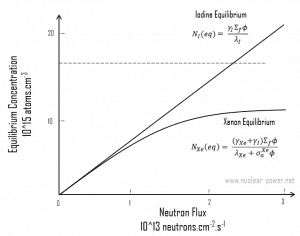
When the rate of production of xenon 135 equals the rate of removal, equilibrium also exists for xenon. The xenon concentration remains constant and is designated NXe(eq). The following equation (1) for the xenon equilibrium concentration can be determined from the preceding equation by setting the dNXe/dt =0. For xenon 135 to be in equilibrium, iodine 135 must also be in equilibrium. Substituting the expression for equilibrium iodine 135 concentration into the equation for equilibrium xenon (1) results in the following (2).
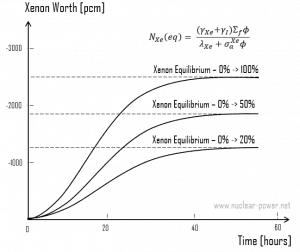 This equation shows that the equilibrium value for xenon 135 increases as power increases because the numerator is proportional to the fission reaction rate. But the thermal flux is also in the denominator. Therefore, as the thermal flux exceeds some value, the xenon burnup begins to dominate, and at approximately 1015 neutrons.cm-2.s-1, the xenon-135 concentration approaches a limiting value. The equilibrium iodine 135 and xenon 135 concentrations as a function of neutron flux are illustrated in the following figure.
This equation shows that the equilibrium value for xenon 135 increases as power increases because the numerator is proportional to the fission reaction rate. But the thermal flux is also in the denominator. Therefore, as the thermal flux exceeds some value, the xenon burnup begins to dominate, and at approximately 1015 neutrons.cm-2.s-1, the xenon-135 concentration approaches a limiting value. The equilibrium iodine 135 and xenon 135 concentrations as a function of neutron flux are illustrated in the following figure.