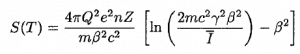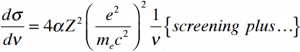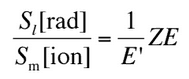Each type of particle interacts differently. Therefore we must describe the interaction of particles (radiation as a flow of these particles) separately. For example, charged particles with high energies can directly ionize atoms. On the other hand, electrically neutral particles interact indirectly and transfer some or all of their energies to the matter. This is the key feature of the categorization of radiation sources. They are usually categorized into two general types as follows:
- Charged particles (directly ionizing)
- Beta particles. Beta particles are fast electrons or positrons emitted in nuclear beta decay, as well as energetic electrons produced by any other process.
- Heavy charged particles. Heavy charged particles are all energetic ions with one atomic mass unit or greater mass, such as protons, alpha particles (helium nuclei), or fission fragments.
- Neutral particles (indirectly ionizing)
- Photon radiation (electromagnetic radiation). Photons are particles/waves (Wave-Particle Duality) without rest mass or electrical charge. Also visible light is electromagnetic radiation, but with much lower energies. The electromagnetic radiation of interest includes X-rays emitted in the rearrangement of electron shells of atoms and gamma rays emitted from the nucleus.
- Neutrons. Neutrons can be emitted by nuclear fission or by the decay of some radioactive atoms. Neutrons have zero electrical charges and cannot directly cause ionization.
- Neutrinos. Neutrinos are electrically neutral, weakly interacting elementary particles, which have very low cross sections for any interaction with matter and, therefore, low probabilities for colliding in the matter.
The design of all nuclear reactors and other nuclear systems depends fundamentally on how radiation interacts with matter. This knowledge is very important for the understanding of:
- Neutron Moderation. How neutrons slow down to thermal energies.
- Power Distribution. Where is the energy generated?
- Reactor Power Measurement. How can we measure the reactor power, and how can we control the chain reaction.
- Radiation Shielding. How can we shield all the various types of radiation produced in the reactor core.
In nuclear reactor we can typically encounter with one of following types of radiation:
Description of Alpha Particles
 Alpha particles are energetic nuclei of helium. The production of alpha particles is termed alpha decay. Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. Alpha particles are relatively large and carry a double positive charge. They are not very penetrating, and a piece of paper can stop them. They travel only a few centimeters but deposit all their energies along their short paths. For example, they are produced in the fuel (alpha decay of heavy nuclei) in nuclear reactors. Alpha particles are commonly emitted by all of the heavy radioactive nuclei occurring in nature (uranium, thorium, or radium), as well as the transuranic elements (neptunium, plutonium, or americium). Especially energetic alpha particles (except artificially accelerated helium nuclei) are produced in a nuclear process known as ternary fission. In this process, the uranium nucleus is split into three charged particles (fission fragments) instead of the normal two. The smallest fission fragments most probably (90% probability) is an extra energetic alpha particle.
Alpha particles are energetic nuclei of helium. The production of alpha particles is termed alpha decay. Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. Alpha particles are relatively large and carry a double positive charge. They are not very penetrating, and a piece of paper can stop them. They travel only a few centimeters but deposit all their energies along their short paths. For example, they are produced in the fuel (alpha decay of heavy nuclei) in nuclear reactors. Alpha particles are commonly emitted by all of the heavy radioactive nuclei occurring in nature (uranium, thorium, or radium), as well as the transuranic elements (neptunium, plutonium, or americium). Especially energetic alpha particles (except artificially accelerated helium nuclei) are produced in a nuclear process known as ternary fission. In this process, the uranium nucleus is split into three charged particles (fission fragments) instead of the normal two. The smallest fission fragments most probably (90% probability) is an extra energetic alpha particle.
Description of Fission Fragments
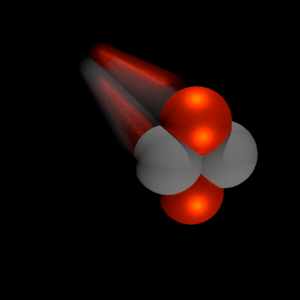
Nuclear fission fragments are the fragments left after a nucleus fissions. Typically, when the uranium 235 nucleus undergoes fission, the nucleus splits into two smaller nuclei, along with a few neutrons, and releases energy in the form of heat (kinetic energy of these fission fragments) and gamma rays. The average of the fragment mass is about 118, but very few fragments near that average are found. It is much more probable to break up into unequal fragments, and the most probable fragment masses are around mass 95 (Krypton) and 137 (Barium).
Most of these fission fragments are highly unstable (radioactive) and undergo further radioactive decays to stabilize themselves. Fission fragments interact strongly with the surrounding atoms or molecules traveling at high speed, causing them to ionize.
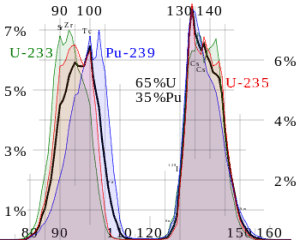
Most energy released by one fission (~160MeV of total ~200MeV) appears as kinetic energy of the fission fragments.
Nature of Interaction of Charged Particles with Matter
Since the electromagnetic interaction extends over some distance, it is not necessary for the light or heavy charged particle to make a direct collision with an atom. These particles can transfer energy simply by passing close by. Heavy charged particles, such as fission fragments or alpha particles, interact with matter primarily through coulomb forces between their positive charge and the negative charge of the electrons from atomic orbitals. On the other hand, the internal energy of an atom is quantized. Therefore an only a certain amount of energy can be transferred. In general, charged particles transfer energy mostly by:
- Excitation. The charged particle can transfer energy to the atom, raising electrons to higher energy levels.
- Ionization. Ionization can occur when the charged particle has enough energy to remove an electron. This results in the creation of ion pairs in surrounding matter.

The creation of pairs requires energy, which is lost from the kinetic energy of the charged particle, causing it to decelerate. The positive ions and free electrons created by the passage of the charged particle will then reunite, releasing energy in the form of heat (e.g.,, vibrational energy or rotational energy of atoms). This is the principle of how fission fragments heat fuel in the reactor core. There are considerable differences in the ways of energy loss and scattering between the passage of light-charged particles such as positrons and electrons and heavy charged particles such as fission fragments, alpha particles, muons. Most of these differences are based on the different dynamics of the collision process. In general, when a heavy particle collides with a much lighter particle (electrons in the atomic orbitals), the laws of energy and momentum conservation predict that only a small fraction of the massive particle’s energy can be transferred to the less massive particle. The actual amount of transferred energy depends on how closely the charged particles pass through the atom, and it also depends on restrictions from the quantization of energy levels.
The distance required to bring the particle to rest referred to as its range. The range of fission fragments in solids amounts to only a few microns, and thus most of the energy of fission is converted to heat very close to the point of fission. In the case of gases, the range increases to a few centimeter’s independence of gas parameters (density, type of gas, etc.) The trajectory of heavy charged particles is not greatly affected because they interact with light atomic electrons. Other charged particles, such as the alpha particles, behave similarly with one exception – for lighter charged particles, the ranges are somewhat longer.
Stopping Power – Bethe Formula
A convenient variable that describes the ionization properties of the surrounding medium is the stopping power. The linear stopping power of the material is defined as the ratio of the differential energy loss for the particle within the material to the corresponding differential path length: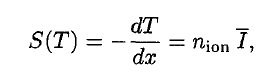
Where T is the kinetic energy of the charged particle, nion is the number of electron-ion pairs formed per unit path length, and I denotes the average energy needed to ionize an atom in the medium. For charged particles, S increases as the particle velocity decreases. The classical expression that describes the specific energy loss is known as the Bethe formula. Hans Bethe found the non-relativistic formula in 1930. He also found the relativistic version (see below) in 1932.
In this expression, m is the rest mass of the electron, β equals v/c, which expresses the particle’s velocity relative to the speed of light, γ is the Lorentz factor of the particle, Q equals to its charge, Z is the atomic number of the medium and n is the density of the atoms in the volume. For non-relativistic particles (heavy charged particles are mostly non-relativistic), dT/dx is dependent on 1/v2. This can be explained by the greater time the charged particle spends in the negative field of the electron when the velocity is low.
The stopping power of most materials is very high for heavy-charged particles, and these particles have very short ranges. For example, a 5 MeV alpha particle’s range is approximately 0,002 cm in aluminium alloy. Most alpha particles can be stopped by an ordinary sheet of paper or living tissue. Therefore the shielding of alpha particles does not pose a difficult problem. On the other hand, alpha radioactive nuclides can lead to serious health hazards when ingested or inhaled (internal contamination).
Specifics of Fission Fragments
The fission fragments have three key features (somewhat different from alpha particles or protons), which influence their energy loss during travel through matter.
- High initial energy. Results in a large effective charge.
- Large effective charge. The fission fragments start with a lack of many electrons. Therefore their specific loss is greater than alpha’s specific loss, for example.
- Immediate electron pickup. Results in changes of (-dE/dx) during the travel.
These features result in the continuous decrease in the effective charge carried by the fission fragment as the fragment comes to rest and a continuous decrease in -dE/dx. The resulting decrease in -dE/dx (from the electron pickup) is larger than the increase that accompanies a reduction in velocity. The range of a typical fission fragment can be approximately half that of a 5 MeV alpha particle.
Bragg Curve
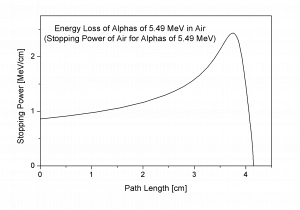
Source: wikipedia.org
The Bragg curve is typical for heavy-charged particles and describes the energy loss of ionizing radiation during travel through matter. This curve is typical of the Bragg peak, which results from 1/v2 dependency of the stopping power. This peak occurs because the cross-section of interaction increases immediately before the particle comes to rest. The charge remains unchanged for most of the track, and the specific energy loss increases according to the 1/v2. Near the end of the track, the charge can be reduced through electron pickup, and the curve can fall off.
The Bragg curve also differs somewhat due to the effect of straggling. For a given material, the range will be nearly the same for all particles of the same kind with the same initial energy. Because the details of the microscopic interactions undergone by any specific particle vary randomly, a small variation in the range can be observed. This variation is called straggling, and it is caused by the statistical nature of the energy loss process, which consists of many individual collisions.
This phenomenon, described by the Bragg curve, is exploited in particle therapy of cancer because this allows concentrating the stopping energy on the tumor while minimizing the effect on the surrounding healthy tissue.
See also: Interaction of Heavy Charged Particles with Matter
Description Beta Particles
Beta particles are high-energy, high-speed electrons or positrons emitted by certain fission fragments or certain primordial radioactive nuclei such as potassium-40. The beta particles are a form of ionizing radiation, also known as beta rays. The production of beta particles is termed beta decay. There are two forms of beta decay, electron decay (β− decay) and positron decay (β+ decay). A nuclear reactor occurs especially the β− decay because the common feature of the fission products is an excess of neutrons (see Nuclear Stability). An unstable fission fragment with the excess of neutrons undergoes β− decay, where the neutron is converted into a proton, an electron, and an electron antineutrino.
The spectrum of beta particles
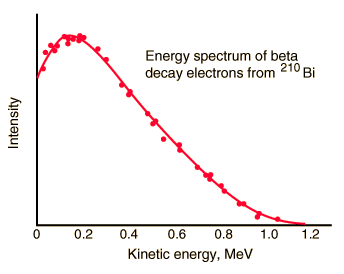
In the process of beta decay, either an electron or a positron is emitted. This emission is accompanied by antineutrino (β- decay) or neutrino (β+ decay), which shares energy and momentum of the decay. The beta emission has a characteristic spectrum. This characteristic spectrum is caused by the fact that either a neutrino or an antineutrino is emitted with the emission of the beta particles. The shape of this energy curve depends on what fraction of the reaction energy (Q value-the amount of energy released by the reaction) is carried by the massive particle. Beta particles can therefore be emitted with any kinetic energy ranging from 0 to Q. By 1934, Enrico Fermi had developed a Fermi theory of beta decay, which predicted the shape of this energy curve.
Nature of Interaction of Beta Radiation with Matter
Summary of types of interactions:
- Inelastic collisions with atomic electrons (Excitation and Ionization)
- Elastic scattering off nuclei
- Bremsstrahlung.
- Cherenkov radiation.
- Annihilation (only positrons)

The nature of the interaction of beta radiation with matter is different from alpha radiation, even though beta particles are also charged particles. Beta particles have a much lower mass compared with alpha particles, and they reach mostly relativistic energies. Its mass is equal to the mass of the orbital electrons with which they are interacting. A much larger fraction of its kinetic energy can be lost in a single interaction than the alpha particle. Since the beta particles mostly reach relativistic energies, the non-relativistic Bethe formula cannot be used. For high-energy electrons, a similar expression has also been derived by Bethe to describe the specific energy loss due to excitation and ionization (the “collisional losses”).
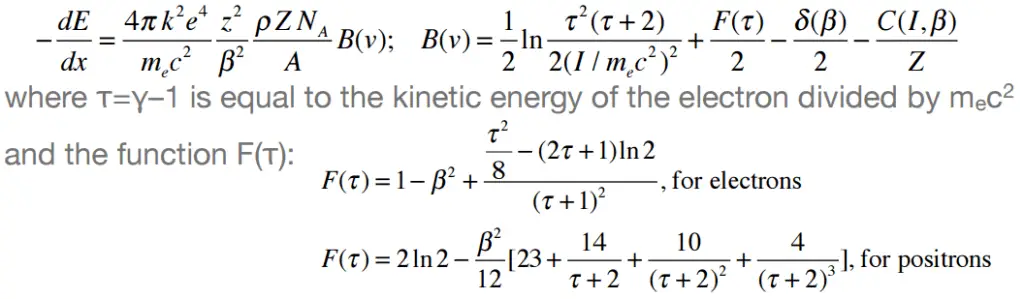
Moreover, beta particles can interact via electron-nuclear interaction (elastic scattering off nuclei), which can significantly change the direction of a beta particle. Therefore their path is not so straightforward. The beta particles follow a very zig-zag path through absorbing material. This resulting path of the particle is longer than the linear penetration (range) into the material.
Beta particles differ from other heavy charged particles in the fraction of energy lost by the radiative process known as the bremsstrahlung. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy, and the deceleration radiation is known as the bremsstrahlung (“braking radiation”).
There is another mechanism by which beta particles lose energy via the production of electromagnetic radiation. When the beta particle moves faster than the speed of light (phase velocity) in the material, it generates a shock wave of electromagnetic radiation known as the Cherenkov radiation.
Positrons interact similarly with the matter when they are energetic. But when the positron comes to rest, it interacts with a negatively charged electron, resulting in the annihilation of the electron-positron pair.
Bremsstrahlung
The bremsstrahlung is electromagnetic radiation produced by the acceleration or deceleration of a charged particle when deflected by magnetic fields (an electron by a magnetic field of particle accelerator) or another charged particle (an electron by an atomic nucleus). The name bremsstrahlung comes from German. The literal translation is ‘braking radiation’. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy.
The bremsstrahlung is possible interactions of light-charged particles with matter (especially with high atomic numbers).
The two commonest occurrences of bremsstrahlung are by:
- Deceleration of charged particle. When charged particles enter a material, they are decelerated by the electric field of the atomic nuclei and atomic electrons.
- Acceleration of charged particle. When ultra-relativistic charged particles move through magnetic fields, they are forced to move along a curved path. Since their direction of motion is continually changing, they are also accelerating and so emit bremsstrahlung. In this case, it is referred to as synchrotron radiation.
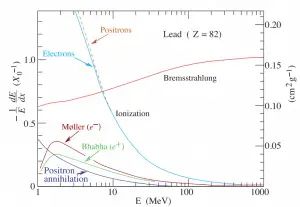
function of electron or positron energy. Source: http://pdg.lbl.gov/
Since the bremsstrahlung is much stronger for lighter particles, this effect is more important for beta particles than protons, alpha particles, and heavy charged nuclei (fission fragments). This effect can be neglected at particle energies below 1 MeV because the energy loss due to bremsstrahlung is very small. Radiation loss starts to become important only at particle energies well above the minimum ionization energy. At relativistic energies, the ratio of loss rate by bremsstrahlung to loss rate by ionization is approximately proportional to the product of the particle’s kinetic energy and the atomic number of the absorber.
The cross-section of bremsstrahlung depends on mostly these terms:
So the ratio of stopping powers of bremsstrahlung and ionization losses is:
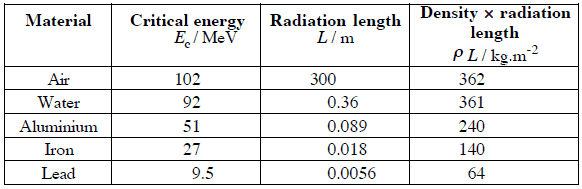
Where E is the particle’s (electron’s) kinetic energy, Z is the mean atomic number of the material, and E’ is a proportionality constant; E’ ≈ 800 MeV. The kinetic energy at which energy loss by bremsstrahlung is equal to the energy loss by ionization and excitation (collisional losses) is called the critical energy. Another parameter is the radiation length, defined as the distance over which the incident electron’s energy is reduced by a factor of 1/e (0.37) due to radiation losses alone. The following table gives some typical values:
Cherenkov Radiation
Cherenkov radiation is electromagnetic radiation emitted when a charged particle (such as an electron) moves through a dielectric medium faster than the phase velocity of light in that medium. It is similar to the bow wave produced by a boat traveling faster than water waves. Cherenkov radiation only occurs if the particle’s speed is higher than the phase velocity of light in the material. Even at high energies, the energy lost by Cherenkov radiation is much less than the other mechanisms (collisions, bremsstrahlung). It is named after Soviet physicist Pavel Alekseyevich Cherenkov, who shared the Nobel Prize in physics in 1958 with Ilya Frank and Igor Tamm to discover Cherenkov radiation, made in 1934.


Cherenkov radiation can be used to detect high-energy charged particles (especially beta particles). Beta particles (high-energy electrons) are released as the fission fragments decay in nuclear reactors or a spent nuclear fuel pool. The glow is visible also after the chain reaction stops (in the reactor). The Cherenkov radiation can characterize the remaining radioactivity of spent nuclear fuel. Therefore it can be used for measuring fuel burnup.
Positron Interactions
 The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with the matter when they are energetic. The track of positrons in a material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.
The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with the matter when they are energetic. The track of positrons in a material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.
At the end of their path, positrons differ significantly from electrons. When a positron (antimatter particle) comes to rest, it interacts with an electron (matter particle), resulting in the annihilation of both particles and the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
Positron Annihilation
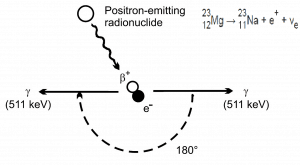
Electron–positron annihilation occurs when a negatively charged electron and a positively charged positron collide. When a low-energy electron annihilates a low-energy positron (the electron’s antiparticle), they can only produce two or more photons (gamma rays). The production of only one photon is forbidden because of the conservation of linear momentum and total energy. The production of another particle is also forbidden because both particles (electron-positron) together do not carry enough mass energy to produce heavier particles. When an electron and a positron collide, they annihilate, resulting in the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
e− + e+ → γ + γ (2x 0.511 MeV)
This process must satisfy some conservation laws, including:
- Conservation of electric charge. The net charge before and after is zero.
- Conservation of linear momentum and total energy. T
- Conservation of angular momentum.
See also: Interaction of Beta Radiation with Matter.
-
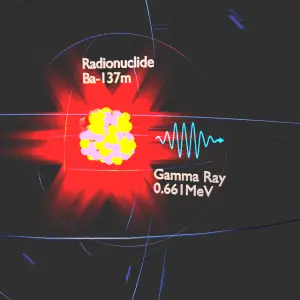
Barium-137m is a product of a common fission product – Caesium – 137. The main gamma-ray of Barium-137m is 661keV photon. Gamma rays are high-energy photons (about 10 000 times as much energy as the visible photons), the same photons as the photons forming the visible range of the electromagnetic spectrum – light.
- Photons (gamma rays and X-rays) can ionize atoms directly (despite they are electrically neutral) through the Photoelectric effect and the Compton effect, but secondary (indirect) ionization is much more significant.
- Gamma rays ionize matter primarily via indirect ionization.
- Although many possible interactions are known, there are three key interaction mechanisms with the matter.
- Gamma rays travel at the speed of light, and they can travel thousands of meters in the air before spending their energy.
- Since gamma radiation is very penetrating, it must be shielded by very dense materials, such as lead or uranium.
- The distinction between X-rays and gamma rays is not so simple and has changed in recent decades. According to the currently valid definition, X-rays are emitted by electrons outside the nucleus, while the nucleus emits gamma rays.
- Gamma rays frequently accompany the emission of alpha and beta radiation.
See also: Interaction of Gamma Radiation with Matter
Photoelectric Effect
Key Characteristics
-

Photoelectric effect with photons from visible spectrum on potassium plate – threshold energy – 2eV The photoelectric effect dominates at low-energies of gamma rays.
- The photoelectric effect leads to the emission of photoelectrons from matter when light (photons) shines upon them.
- The maximum energy an electron can receive in any one interaction is hν.
- The photoelectric effect only emits electrons if the photon reaches or exceeds threshold energy.
- A free-electron (e.g.,, from an atomic cloud) cannot absorb the entire energy of the incident photon. This is a result of the need to conserve both momentum and energy.
- The cross-section for the emission of n=1 (K-shell) photoelectrons is higher than that of n=2 (L-shell) photoelectrons. This is a result of the need to conserve momentum and energy.
See also: Albert Einstein and the Photoelectric Effect
See also: Photoelectric Effect
Definition of Photoelectric Effect
Source: laradioactivite.com/
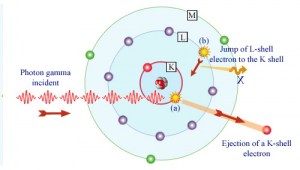
In the photoelectric effect, a photon undergoes an interaction with an electron that is bound in an atom. The incident photon completely disappears in this interaction, and the atom ejects an energetic photoelectron from one of its bound shells. The kinetic energy of the ejected photoelectron (Ee) is equal to the incident photon energy (hν) minus the binding energy of the photoelectron in its original shell (Eb).
Ee=hν-Eb
Therefore, photoelectrons are only emitted by the photoelectric effect if the photon reaches or exceeds threshold energy – the electron’s binding energy – the material’s work function. For gamma rays with energies of more than hundreds keV, the photoelectron carries off the majority of the incident photon energy – hν.
Following a photoelectric interaction, an ionized absorber atom is created with a vacancy in one of its bound shells. An electron from a shell will quickly fill this vacancy with lower binding energy (other shells) or capture a free electron from the material. The rearrangement of electrons from other shells creates another vacancy, which, in turn, is filled by an electron from an even lower binding energy shell. Therefore a cascade of more characteristic X-rays can also be generated. The probability of characteristic x-ray emission decreases as the atomic number of the absorber decreases. Sometimes, the emission of an Auger electron occurs.
Compton Scattering
Key Characteristics
- Compton scattering dominates at intermediate energies.
- It is the scattering of photons by atomic electrons
- Photons undergo a wavelength shift called the Compton shift.
- The energy transferred to the recoil electron can vary from zero to a large fraction of the incident gamma-ray energy.
See also: Compton Scattering
See also: Compton Scattering – Cross-Sections
See also: Inverse Compton Scattering
Definition of Compton Scattering
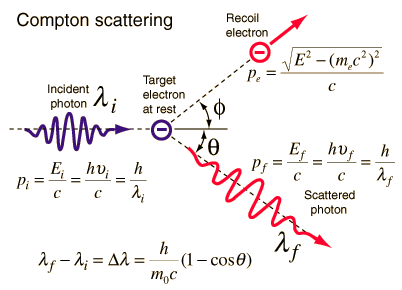
Source: hyperphysics.phy-astr.gsu.edu
Compton scattering is the inelastic or nonclassical scattering of a photon (which may be an X-ray or gamma-ray photon) by a charged particle, usually an electron. In Compton scattering, the incident gamma-ray photon is deflected through an angle Θ with regard to its original direction. This deflection decreases the photon’s frequency’s energy (decrease in photon’s frequency) and is called the Compton effect. The photon transfers a portion of its energy to the recoil electron. The energy transferred to the recoil electron can vary from zero to a large fraction of the incident gamma-ray energy because all scattering angles are possible. A. H.Compton observed the Compton scattering in 1923 at Washington University in St. Louis. Compton earned the Nobel Prize in Physics in 1927 for this new understanding of the particle nature of photons.
See also: Compton Formula
Pair Production
 In general, pair production is a phenomenon of nature where energy is directly converted to matter. The phenomenon of pair production can be view two different ways. One way is as a particle and antiparticle, and the other is as a particle and a hole. The first
In general, pair production is a phenomenon of nature where energy is directly converted to matter. The phenomenon of pair production can be view two different ways. One way is as a particle and antiparticle, and the other is as a particle and a hole. The first
way can be represented by the formation of electrons and positrons from a packet of electromagnetic energy (high energy photon – gamma-ray) traveling through matter. It is one of the possible ways in which gamma rays interact with matter. At high energies, this interaction dominates.
For electron-positron pair production to occur, the electromagnetic energy of the photon must be above threshold energy, which is equivalent to the rest mass of two electrons. The threshold energy (the total rest mass of produced particles) for electron-positron pair production equals 1.02MeV (2 x 0.511MeV) because the rest mass of a single electron is equivalent to 0.511MeV of energy.
If the original photon’s energy is greater than 1.02MeV, any energy above 1.02MeV is, according to the conservation law, split between the kinetic energy of motion of the two particles.
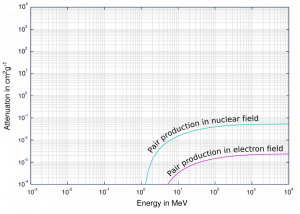
The presence of an electric field of a heavy atom such as lead or uranium is essential to satisfy the conservation of momentum and energy. The atomic nucleus must receive some momentum to satisfy both conservations of momentum and energy. Therefore a photon pair production in free space cannot occur.
Moreover, the positron is the antiparticle of the electron, so when a positron comes to rest, it interacts with another electron, resulting in the annihilation of both particles and the complete conversion of their rest mass back to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons). The pair production phenomenon is therefore connected with the creation and destruction of matter in one reaction.
See also: Pair Production
Neutron interactions
Neutrons are neutral particles. Therefore they travel in straight lines, deviating from their path only when they collide with a nucleus to be scattered into a new direction or absorbed. Neither the electrons surrounding (atomic electron cloud) a nucleus nor the electric field caused by a positively charged nucleus affect a neutron’s flight. In short, neutrons collide with nuclei, not with atoms. A defining feature of the transmission of neutrons through bulk matter is the mean free path length (λ – lambda), the mean distance a neutron travels between interactions. It can be calculated from the following equation:
λ=1/Σ
Neutrons may interact with nuclei in one of the following ways:
Neutron cross-section
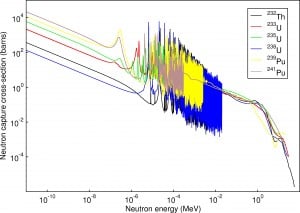
The extent to which neutrons interact with nuclei is described in terms of quantities known as cross-sections. Cross-sections are used to express the likelihood of particular interaction between an incident neutron and a target nucleus. It must be noted this likelihood does not depend on real target dimensions. In conjunction with the neutron flux, it enables the calculation of the reaction rate, for example, to derive the thermal power of a nuclear power plant. The standard unit for measuring the microscopic cross-section (σ-sigma) is the barn, equal to 10-28 m2. This unit is very small. Therefore barns (abbreviated as “b”) are commonly used. The microscopic cross-section can be interpreted as the effective ‘target area’ that a nucleus interacts with an incident neutron.
A macroscopic cross-section is derived from microscopic and the material density:
Σ=σ.N
Here σ, which has units of m2, is referred to as the microscopic cross-section. Since the units of N (nuclei density) are nuclei/m3, the macroscopic cross-section Σ has units of m-1. Thus, it is an incorrect name because it is not a correct unit of cross-sections.
Neutron cross-sections constitute key parameters of nuclear fuel. Neutron cross-sections must be calculated for new fuel assemblies, usually in two-Dimensional models of the fuel lattice.
The neutron cross-section is variable and depends on:
- Target nucleus (hydrogen, boron, uranium, etc.) Each isotope has its own set of cross-sections.
- Type of the reaction (capture, fission, etc.). Cross-sections are different for each nuclear reaction.
- Neutron energy (thermal neutron, resonance neutron, fast neutron). For a given target and reaction type, the cross-section is strongly dependent on the neutron energy. In the common case, the cross-section is usually much larger at low energies than at high energies. This is why most nuclear reactors use a neutron moderator to reduce the neutron’s energy and thus increase the probability of fission, essential to produce energy and sustain the chain reaction.
- Target energy (temperature of target material – Doppler broadening) This dependency is not so significant. Still, the target energy strongly influences the inherent safety of nuclear reactors due to a Doppler broadening of resonances.
See also: JANIS (Java-based nuclear information software)
See also: Neutron cross-section
Typical cross-sections of materials in the reactor
The following table shows neutron cross-sections of the most common isotopes of the reactor core.
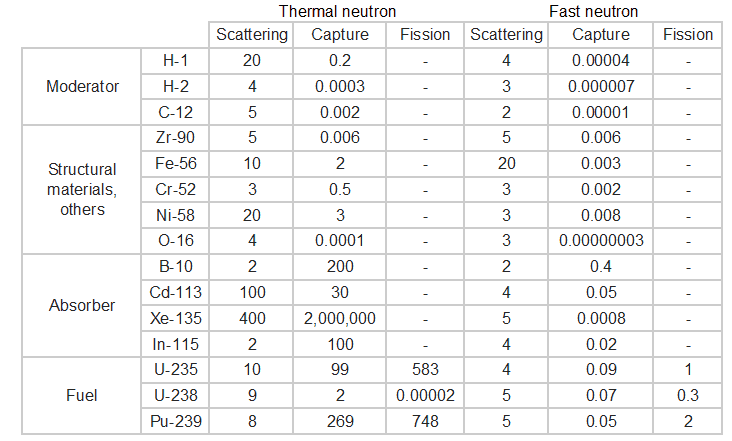

Photo: Roy Kaltschmidt, LBNL
Source: Daya Bay Reactor Neutrino Experiment
Nuclear reactors are the major source of human-generated antineutrinos. This is due to the fact that antineutrinos are produced in negative beta decay. A nuclear reactor occurs especially the β− decay because the common feature of the fission fragments is an excess of neutrons (see Nuclear Stability). An unstable fission fragment with the excess of neutrons undergoes β− decay, where the neutron is converted into a proton, an electron, and an electron antineutrino. The existence of emission of antineutrinos and their very low cross-section for any interaction leads to a very interesting phenomenon.
Roughly about 5% (or about 12 MeV of 207 MeV) of released energy per one fission is radiated away from the reactor in the form of antineutrinos. For a typical nuclear reactor with thermal power of 3000 MWth (~1000MWe of electrical power), the total power produced is higher, approximately 3150 MW, of which 150 MW is radiated away into space as antineutrino radiation. This amount of energy is forever lost since antineutrinos can penetrate all reactor materials without any interaction. In fact, a common statement in physics texts is that the mean free path of a neutrino is approximately a light-year of lead.

Moreover, a neutrino of moderate energy can easily penetrate a thousand light-years of lead (according to J. B. Griffiths).
Please note that billions of solar neutrinos per second pass (mostly without any interaction) through every square centimeter (~6×1010) on the Earth’s surface and antineutrino radiation is by no means dangerous.
Example – Amount of antineutrinos produced:
Stable nuclei with most likely mass number A from U-235 fission are and
. These nuclei have together 98 protons and 136 neutrons, while fission fragments (parent nuclei) have together 92 protons and 142 neutrons. This means the fission fragments must undergo on average 6 negative beta decays (6 neutrons must decay to 6 protons), and therefore 6 antineutrinos must be produced per each fission after each U-235 fission. The typical nuclear reactor therefore produces approximately 6 x 1020 antineutrinos per second (~200 MeV/fission; ~6 antineutrinos/fission; 3000 MWth; 9.375 x 1019 fissions/sec).
Reference: Griffiths, David, Introduction to Elementary Particles, Wiley, 1987.
Knoll, Glenn F., RADIATION DETECTION AND MEASUREMENT, 4th edition
Lamarsh, John R., INTRODUCTION TO NUCLEAR ENGINEERING, 2nd edition