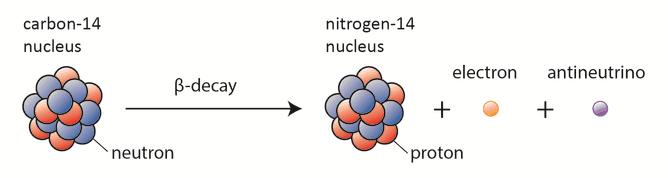
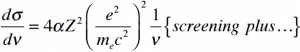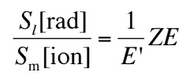Beta particles are high-energy, high-speed electrons or positrons emitted by certain fission fragments or primordial radioactive nuclei such as potassium-40. The beta particles are a form of ionizing radiation, also known as beta rays. The production of beta particles is termed beta decay. There are two forms of beta decay, electron decay (β− decay) and positron decay (β+ decay). A nuclear reactor occurs especially the β− decay because the common feature of the fission products is an excess of neutrons (see Nuclear Stability). An unstable fission fragment with the excess of neutrons undergoes β− decay, where the neutron is converted into a proton, an electron, and an electron antineutrino.
Spectrum of beta particles
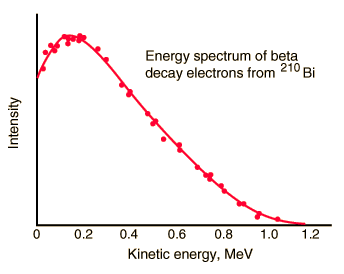
In the process of beta decay, either an electron or a positron is emitted. This emission is accompanied by the emission of antineutrino (β- decay) or neutrino (β+ decay), which shares energy and momentum of the decay. The beta emission has a characteristic spectrum. This characteristic spectrum is caused by the fact that either a neutrino or an antineutrino is emitted with the emission of a beta particle. The shape of this energy curve depends on what fraction of the reaction energy (Q value-the amount of energy released by the reaction) is carried by the massive particle. Beta particles can therefore be emitted with any kinetic energy ranging from 0 to Q. By 1934, Enrico Fermi had developed a Fermi theory of beta decay, which predicted the shape of this energy curve.
Nature of Interaction of Beta Radiation with Matter
Summary of types of interactions:
- Inelastic collisions with atomic electrons (Excitation and Ionization)
- Elastic scattering off nuclei
- Bremsstrahlung.
- Cherenkov radiation.
- Annihilation (only positrons)

The interaction of beta radiation with matter is different from alpha radiation, even though beta particles are also charged particles. Beta particles have a much lower mass compared with alpha particles, and they reach mostly relativistic energies. Their mass is equal to the mass of the orbital electrons with which they are interacting. A much larger fraction of its kinetic energy can be lost in a single interaction than the alpha particle. Since the beta particles mostly reach relativistic energies, the nonrelativistic Bethe formula cannot be used. For high-energy electrons, a similar expression has also been derived by Bethe to describe the specific energy loss due to excitation and ionization (the “collisional losses”).
Moreover, beta particles can interact via electron-nuclear interaction (elastic scattering off nuclei), which can significantly change the direction of a beta particle. Therefore their path is not so straightforward. The beta particles follow a very zig-zag path through absorbing material. This resulting path of the particle is longer than the linear penetration (range) into the material.
Beta particles differ from other heavy charged particles in the fraction of energy lost by the radiative process known as the bremsstrahlung. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy, and the deceleration radiation is known as the bremsstrahlung (“braking radiation”).
There is another mechanism by which beta particles loos energy via the production of electromagnetic radiation. When the beta particle moves faster than the speed of light (phase velocity) in the material, it generates a shock wave of electromagnetic radiation known as the Cherenkov radiation.
Positrons interact similarly with the matter when they are energetic. But when the positron comes to rest, it interacts with a negatively charged electron, resulting in the annihilation of the electron-positron pair.
Bremsstrahlung
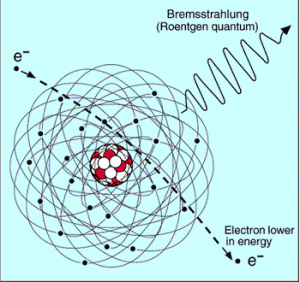
The bremsstrahlung is electromagnetic radiation produced by the acceleration or deceleration of a charged particle when deflected by magnetic fields (an electron by a magnetic field of particle accelerator) or another charged particle (an electron by an atomic nucleus). The name bremsstrahlung comes from German. The literal translation is ‘braking radiation’. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy.
The bremsstrahlung is possible interactions of light-charged particles with matter (especially with high atomic numbers).
The two commonest occurrences of bremsstrahlung are by:
- Deceleration of charged particle. When charged particles enter a material, they are decelerated by the electric field of the atomic nuclei and atomic electrons.
- Acceleration of charged particles. When ultra-relativistic charged particles move through magnetic fields, they are forced to move along a curved path. Since their direction of motion is continually changing, they are also accelerating and so emit bremsstrahlung. In this case, it is referred to as synchrotron radiation.
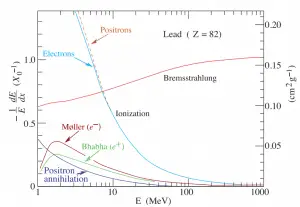
function of electron or positron energy. Source: http://pdg.lbl.gov/
Since the bremsstrahlung is much stronger for lighter particles, this effect is more important for beta particles than protons, alpha particles, and heavy charged nuclei (fission fragments). This effect can be neglected at particle energies below 1 MeV because the energy loss due to bremsstrahlung is very small. Radiation loss starts to become important only at particle energies well above the minimum ionization energy. At relativistic energies, the ratio of loss rate by bremsstrahlung to loss rate by ionization is approximately proportional to the product of the particle’s kinetic energy and the atomic number of the absorber.
The cross-section of bremsstrahlung depends on mostly these terms:
So the ratio of stopping powers of bremsstrahlung and ionization losses is:
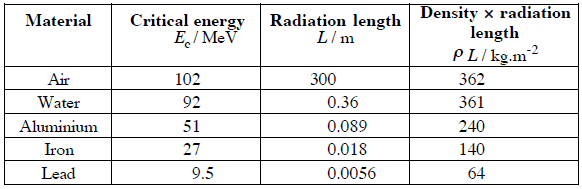
Where E is the particle’s (electron’s) kinetic energy, Z is the mean atomic number of the material, and E’ is a proportionality constant; E’ ≈ 800 MeV. The kinetic energy at which energy loss by bremsstrahlung is equal to the energy loss by ionization and excitation (collisional losses) is called the critical energy. Another parameter is the radiation length, defined as the distance over which the incident electron’s energy is reduced by a factor of 1/e (0.37) due to radiation losses alone. The following table gives some typical values:
Cherenkov Radiation
Cherenkov radiation is electromagnetic radiation emitted when a charged particle (such as an electron) moves through a dielectric medium faster than the phase velocity of light in that medium. It is similar to the bow wave produced by a boat traveling faster than the speed of water waves. Cherenkov radiation only occurs if the particle’s speed is higher than the phase velocity of light in the material. Even at high energies, the energy lost by Cherenkov radiation is much less than the other mechanisms (collisions, bremsstrahlung). It is named after Soviet physicist Pavel Alekseyevich Cherenkov, who shared the Nobel Prize in physics in 1958 with Ilya Frank and Igor Tamm to discover Cherenkov radiation, made in 1934.


Cherenkov radiation can be used to detect high-energy charged particles (especially beta particles). Beta particles (high-energy electrons) are released as the fission fragments decay in nuclear reactors or a spent nuclear fuel pool. The glow is visible also after the chain reaction stops (in the reactor). The Cherenkov radiation can characterize the remaining radioactivity of spent nuclear fuel. Therefore it can be used for measuring fuel burnup.
Positron Interactions
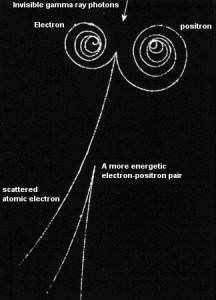 The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with the matter when they are energetic. The track of positrons in the material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.
The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with the matter when they are energetic. The track of positrons in the material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.
At the end of their path, positrons differ significantly from electrons. When a positron (antimatter particle) comes to rest, it interacts with an electron (matter particle), resulting in the annihilation of both particles and the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
Positron Annihilation
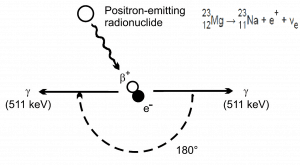
Electron–positron annihilation occurs when a negatively charged electron and a positively charged positron collide. When a low-energy electron annihilates a low-energy positron (the electron’s antiparticle), they can only produce two or more photons (gamma rays). The production of only one photon is forbidden because of the conservation of linear momentum and total energy. The production of another particle is also forbidden because both particles (electron-positron) together do not carry enough mass energy to produce heavier particles. When an electron and a positron collide, they annihilate, resulting in the complete conversion of their rest mass to pure energy (according to the E=mc2 formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).
e− + e+ → γ + γ (2x 0.511 MeV)
This process must satisfy some conservation laws, including:
- Conservation of electric charge. The net charge before and after is zero.
- Conservation of linear momentum and total energy. T
- Conservation of angular momentum.