Compton Scattering
Compton Scattering Formula
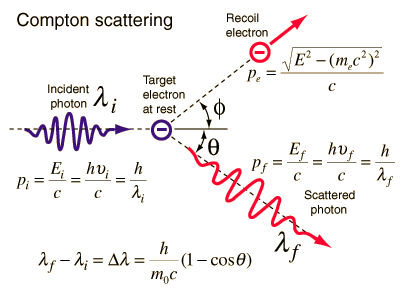
Source: hyperphysics.phy-astr.gsu.edu
The Compton formula was published in 1923 in the Physical Review. Compton explained that the particle-like momentum of photons causes the X-ray shift. Compton scattering formula is the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays. In the case of Compton scattering, the photon of frequency f collides with an electron at rest. The photon bounces off the electron upon collision, giving up some of its initial energy (given by Planck’s formula E=hf). While the electron gains momentum (mass x velocity), the photon cannot lower its velocity. As a result of momentum conservation law, the photon must lower its momentum given by: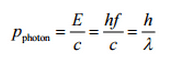 So the decrease in photon’s momentum must be translated into a decrease in frequency (increase in wavelength Δλ = λ’ – λ). The shift of the wavelength increased with scattering angle according to the Compton formula:
So the decrease in photon’s momentum must be translated into a decrease in frequency (increase in wavelength Δλ = λ’ – λ). The shift of the wavelength increased with scattering angle according to the Compton formula: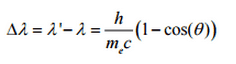 whereλ is the initial wavelength of photonλ’ is the wavelength after scattering,h is the Planck constant = 6.626 x 10-34 J.sme is the electron rest mass (0.511 MeV)c is the speed of lightΘ is the scattering angle. The minimum change in wavelength (λ′ − λ) for the photon occurs when Θ = 0° (cos(Θ)=1) and is at least zero. The maximum change in wavelength (λ′ − λ) for the photon occurs when Θ = 180° (cos(Θ)=-1). In this case, the photon transfers to the electron as much momentum as possible. The maximum change in wavelength can be derived from the Compton formula:
whereλ is the initial wavelength of photonλ’ is the wavelength after scattering,h is the Planck constant = 6.626 x 10-34 J.sme is the electron rest mass (0.511 MeV)c is the speed of lightΘ is the scattering angle. The minimum change in wavelength (λ′ − λ) for the photon occurs when Θ = 0° (cos(Θ)=1) and is at least zero. The maximum change in wavelength (λ′ − λ) for the photon occurs when Θ = 180° (cos(Θ)=-1). In this case, the photon transfers to the electron as much momentum as possible. The maximum change in wavelength can be derived from the Compton formula: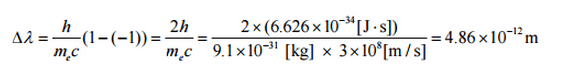 The quantity h/mec is known as the Compton wavelength of the electron and is equal to 2.43×10−12 m.
The quantity h/mec is known as the Compton wavelength of the electron and is equal to 2.43×10−12 m.