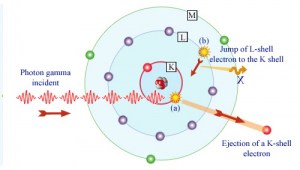
In the photoelectric effect, a photon undergoes an interaction with an electron that is bound in an atom. The incident photon completely disappears in this interaction, and the atom ejects an energetic photoelectron from one of its bound shells. The kinetic energy of the ejected photoelectron (Ee) is equal to the incident photon energy (hν) minus the binding energy of the photoelectron in its original shell (Eb).
Ee=hν-Eb
Therefore, photoelectrons are only emitted by the photoelectric effect if the photon reaches or exceeds threshold energy – the electron’s binding energy – the material’s work function. For gamma rays with energies of more than hundreds keV, the photoelectron carries off the majority of the incident photon energy – hν. Following a photoelectric interaction, an ionized absorber atom is created with a vacancy in one of its bound shells.
Source: laradioactivite.com/
An electron from a shell will quickly fill this vacancy with lower binding energy (other shells) or capture a free electron from the material. The rearrangement of electrons from other shells creates another vacancy, which, in turn, is filled by an electron from an even lower binding energy shell. Therefore a cascade of more characteristic X-rays can also be generated. The probability of characteristic x-ray emission decreases as the atomic number of the absorber decreases. Sometimes, the emission of an Auger electron occurs.
Key Facts
- The photoelectric effect dominates at low-energies of gamma rays.
- The photoelectric effect leads to the emission of photoelectrons from matter when light (photons) shines upon them.
- The maximum energy an electron can receive in any one interaction is hν.
- The photoelectric effect only emits electrons if the photon reaches or exceeds threshold energy.
- A free-electron (e.g.,, from an atomic cloud) cannot absorb the entire energy of the incident photon. This is a result of the need to conserve both momentum and energy.
- The cross-section for the emission of n=1 (K-shell) photoelectrons is higher than that of n=2 (L-shell) photoelectrons. This is a result of the need to conserve momentum and energy.
Source: wikipedia.org
While this is interesting, it is hardly explainable by the classical theory of electromagnetic radiation, which assumed the existence of a stationary medium (the luminiferous aether) through which light propagated. Subsequent investigations into the photoelectric effect result in the fact that these explorations did not fit the classical theory of electromagnetic radiation. In 1905, Albert Einstein published four groundbreaking papers on the photoelectric effect, Brownian motion, special relativity, and the equivalence of mass and energy. These papers were published in the Annalen der Physik journal and contributed significantly to the foundation of modern physics. In the paper on the photoelectric effect (“On a Heuristic Viewpoint Concerning the Production and Transformation of Light”), he solved the paradox by describing light as composed of discrete quanta (German: das Lichtquant) rather than continuous waves. This theory was built on Max Planck’s blackbody radiation theory, which assumes that luminous energy can be absorbed or emitted only in discrete amounts, called quanta. The photon’s energy in each quantum of light is equal to its frequency (ν) multiplied by a constant known as Planck’s constant (h), or alternately, using the wavelength (λ) and the speed of light (c):
E=hc/λ=hν
Each photon above a threshold frequency (specific for each material) has the needed energy to eject a single electron, creating the observed effect. Einstein’s theory predicts that the maximum kinetic energy of the emitted electron is dependent only on the frequency of the incident light and not on its intensity. Shining twice as much light (high-intensity) results in twice as many photons and more electrons releasing, but the maximum kinetic energy of those individual electrons remains the same. Experimentation in the photoelectric effect was carried out extensively by Robert Millikan in 1915. Robert Millikan showed that Einstein’s prediction was correct. This discovery contributed to the quantum revolution in physics and earned Einstein the Nobel Prize in Physics in 1921.
Cross-Sections of Photoelectric Effect
At small values of gamma-ray energy, the photoelectric effect dominates. The mechanism is also enhanced for materials of high atomic number Z. It is not simple to derive an analytic expression for the probability of photoelectric absorption of gamma-ray per atom comprehensive ranges of gamma-ray energies. The probability of photoelectric absorption per unit mass is approximately proportional to:
τ(photoelectric) = constant x ZN/E3.5
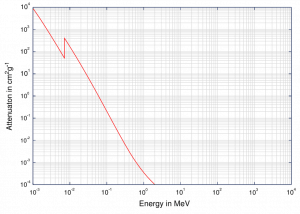where Z is the atomic number, the exponent n varies between 4 and 5. E is the energy of the incident photon. The proportionality to higher powers of the atomic number Z is the main reason for using high Z materials, such as lead or depleted uranium in gamma-ray shields. Although the probability of the photoelectric absorption of gamma photon decreases, in general, with increasing photon energy, there are sharp discontinuities in the cross-section curve. These are called “absorption edges” and correspond to electrons’ binding energies from an atom’s bound shells. For photons with the energy just above the edge, the photon energy is sufficient to undergo the photoelectric interaction with an electron from a bound shell, let say K-shell. The probability of such interaction is just above this edge, much greater than that of photons of energy slightly below this edge. For gamma photons below this edge, the interaction with electrons from K-shell is energetically impossible, and therefore the probability drops abruptly. These edges also occur at binding energies of electrons from other shells (L, M, N …).