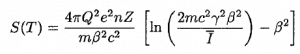Description of Alpha Particles
Alpha particles are energetic nuclei of helium. The production of alpha particles is termed alpha decay. Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. Alpha particles are relatively large and carry a double positive charge. They are not very penetrating, and a piece of paper can stop them. They travel only a few centimeters but deposit all their energies along their short paths. For example, nuclear reactors are produced in the fuel (alpha decay of heavy nuclei). Alpha particles are commonly emitted by all of the heavy radioactive nuclei occurring in nature (uranium, thorium, or radium), as well as the transuranic elements (neptunium, plutonium, or americium). Especially energetic alpha particles (except artificially accelerated helium nuclei) are produced in a nuclear process known as ternary fission. In this process, the uranium nucleus is split into three charged particles (fission fragments) instead of the normal two. The smallest fission fragments most probably (90% probability) is an extra energetic alpha particle.
Description of Fission Fragments
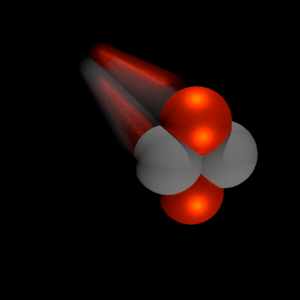
Nuclear fission fragments are the fragments left after a nucleus fissions. Typically, when the uranium 235 nucleus undergoes fission, the nucleus splits into two smaller nuclei, along with a few neutrons, and releases energy in the form of heat (kinetic energy of these fission fragments) and gamma rays. The average of the fragment mass is about 118, but very few fragments near that average are found. It is much more probable to break up into unequal fragments, and the most probable fragment masses are around mass 95 (Krypton) and 137 (Barium).
Most of these fission fragments are highly unstable (radioactive) and undergo further radioactive decays to stabilize themselves. Fission fragments interact strongly with the surrounding atoms or molecules traveling at high speed, causing them to ionize.
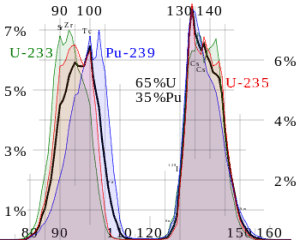
Most energy released by one fission (~160MeV of total ~200MeV) appears as kinetic energy of the fission fragments.
Nature of Interaction of Charged Particles with Matter
Since the electromagnetic interaction extends over some distance, it is not necessary for the light or heavy charged particles to make a direct collision with an atom. These particles can transfer energy simply by passing close by. Heavy charged particles, such as fission fragments or alpha particles, interact with matter primarily through coulomb forces between their positive charge and the negative charge of the electrons from atomic orbitals. On the other hand, the internal energy of an atom is quantized. Therefore only a certain amount of energy can be transferred. In general, charged particles transfer energy mostly by:
- Excitation. The charged particle can transfer energy to the atom, raising electrons to higher energy levels.
- Ionization. Ionization can occur when the charged particle has enough energy to remove an electron. This results in the creation of ion pairs in surrounding matter.
The creation of pairs requires energy, which is lost from the kinetic energy of the charged particle, causing it to decelerate. The positive ions and free electrons created by the passage of the charged particle will then reunite, releasing energy in the form of heat (e.g.,, vibrational energy or rotational energy of atoms). This is the principle of how fission fragments heat fuel in the reactor core. There are considerable differences in the ways of energy loss and scattering between the passage of light-charged particles such as positrons and electrons and heavy charged particles such as fission fragments, alpha particles, muons. Most of these differences are based on the different dynamics of the collision process. In general, when a heavy particle collides with a much lighter particle (electrons in the atomic orbitals), the laws of energy and momentum conservation predict that only a small fraction of the massive particle’s energy can be transferred to the less massive particle. The actual amount of transferred energy depends on how closely the charged particles pass through the atom, and it also depends on restrictions from the quantization of energy levels.
The distance required to bring the particle to rest referred to as its range. The range of fission fragments in solids amounts to only a few microns, and thus most of the energy of fission is converted to heat very close to the point of fission. In the case of gases, the range increases to a few centimeter’s independence of gas parameters (density, type of gas, etc.) The trajectory of heavy charged particles is not greatly affected because they interact with light atomic electrons. Other charged particles, such as the alpha particles, behave similarly with one exception – for lighter charged particles, the ranges are somewhat longer.
Stopping Power – Bethe Formula
A convenient variable that describes the ionization properties of the surrounding medium is the stopping power. The linear stopping power of the material is defined as the ratio of the differential energy loss for the particle within the material to the corresponding differential path length: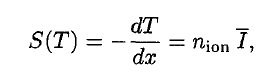
Where T is the kinetic energy of the charged particle, nion is the number of electron-ion pairs formed per unit path length, and I denotes the average energy needed to ionize an atom in the medium. For charged particles, S increases as the particle velocity decreases. The classical expression that describes the specific energy loss is known as the Bethe formula. Hans Bethe found the non-relativistic formula in 1930. Hans Bethe also found the relativistic version (see below) in 1932.
In this expression, m is the rest mass of the electron, β equals v/c, which expresses the particle’s velocity relative to the speed of light, γ is the Lorentz factor of the particle, Q equals to its charge, Z is the atomic number of the medium and n is the density of the atoms in the volume. For non-relativistic particles (heavy charged particles are mostly non-relativistic), dT/dx is dependent on 1/v2. This can be explained by the greater time the charged particle spends in the negative field of the electron when the velocity is low.
The stopping power of most materials is very high for heavy-charged particles, and these particles have very short ranges. For example, a 5 MeV alpha particle’s range is approximately 0,002 cm in aluminium alloy. Most alpha particles can be stopped by an ordinary sheet of paper or living tissue. Therefore the shielding of alpha particles does not pose a difficult problem. On the other hand, alpha radioactive nuclides can lead to serious health hazards when ingested or inhaled (internal contamination).
Specifics of Fission Fragments
The fission fragments have two key features (somewhat different from alpha particles or protons), which influence their energy loss during their travel through matter.
- High initial energy. Results in a large effective charge.
- Large effective charge. The fission fragments start with a lack of many electrons. Therefore their specific loss is greater than alpha’s specific loss, for example.
- Immediate electron pickup. Results in changes of (-dE/dx) during the travel.
These features result in the continuous decrease in the effective charge carried by the fission fragment as the fragment comes to rest and a continuous decrease in -dE/dx. The resulting decrease in -dE/dx (from the electron pickup) is larger than the increase that accompanies a reduction in velocity. The range of a typical fission fragment can be approximately half that of a 5 MeV alpha particle.
Bragg Curve
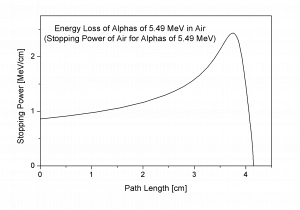
Source: wikipedia.org
The Bragg curve is typical for heavy-charged particles and describes the energy loss of ionizing radiation during travel through matter. This curve is typical of the Bragg peak, which results from 1/v2 dependency of the stopping power. This peak occurs because the cross-section of interaction increases immediately before the particle comes to rest. The charge remains unchanged for most of the track, and the specific energy loss increases according to the 1/v2. Near the end of the track, the charge can be reduced through electron pickup, and the curve can fall off.
The Bragg curve also differs somewhat due to the effect of straggling. For a given material, the range will be nearly the same for all particles of the same kind with the same initial energy. Because the details of the microscopic interactions undergone by any specific particle vary randomly, a small variation in the range can be observed. This variation is called straggling, and it is caused by the statistical nature of the energy loss process, which consists of many individual collisions.
This phenomenon, described by the Bragg curve, is exploited in particle therapy of cancer because this allows concentrating the stopping energy on the tumor while minimizing the effect on the surrounding healthy tissue.
