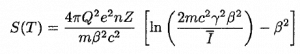A convenient variable that describes the ionization properties of the surrounding medium is the stopping power. The linear stopping power of the material is defined as the ratio of the differential energy loss for the particle within the material to the corresponding differential path length:
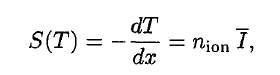
Where T is the kinetic energy of the charged particle, nion is the number of electron-ion pairs formed per unit path length, and I denotes the average energy needed to ionize an atom in the medium. For charged particles, S increases as the particle velocity decreases. The classical expression that describes the specific energy loss is known as the Bethe formula. The non-relativistic formula was be found by Hans Bethe in 1930. Hans Bethe also found the relativistic version (see below) in 1932.
In this expression, m is the rest mass of the electron, β equals v/c, which expresses the particle’s velocity relative to the speed of light, γ is the Lorentz factor of the particle, Q equals to its charge, Z is the atomic number of the medium and n is the density of the atoms in the volume. For non-relativistic particles (heavy charged particles are mostly non-relativistic), dT/dx is dependent on 1/v2. This can be explained by the greater time the charged particle spends in the negative field of the electron when the velocity is low.
The stopping power of most materials is very high for heavy-charged particles, and these particles have very short ranges. For example, the range of a 5 MeV alpha particle is approximately only 0.002 cm in aluminium alloy. Most alpha particles can be stopped by an ordinary sheet of paper or living tissue. Therefore the shielding of alpha particles does not pose a difficult problem. On the other hand, alpha radioactive nuclides can lead to serious health hazards when ingested or inhaled (internal contamination).
Specifics of Fission Fragments
The fission fragments have two key features (somewhat different from alpha particles or protons), which influence their energy loss during travel through matter.
- High initial energy. Results in a large effective charge.
- Large effective charge. The fission fragments start with a lack of many electrons. Therefore their specific loss is greater than alpha’s specific loss, for example.
- Immediate electron pickup. Results in changes of (-dE/dx) during the travel.
These features result in the continuous decrease in the effective charge carried by the fission fragment as the fragment comes to rest and a continuous decrease in -dE/dx. The resulting decrease in -dE/dx (from the electron pickup) is larger than the increase that accompanies a reduction in velocity. The range of a typical fission fragment can be approximately half that of a 5 MeV alpha particle.
See next: