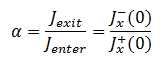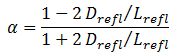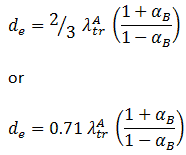It is well known that each reactor core is surrounded by a neutron reflector. The reflector reduces the non-uniformity of the power distribution in the peripheral fuel assemblies, reduces neutron leakage, and reduces a coolant flow bypass of the core. The neutron reflector is a non-multiplying medium, whereas the reactor core is a multiplying medium.
On this special interface, we shall apply an albedo boundary condition to represent the neutron reflector. Albedo, the latin word for “whiteness”, was defined by Lambert as the fraction of the incident light reflected diffusely by a surface.
In reactor engineering, albedo, or the reflection coefficient, is defined as the ratio of exiting to entering neutrons, and we can express it in terms of neutron currents as:
For sufficiently thick reflectors, it can be derived that albedo becomes
where Drefl is the diffusion coefficient in the reflector, and the Lrefl is the reflection’s diffusion length.
If we are not interested in the neutron flux distribution in the reflector (let say in the slab B) but only in the effect of the reflector on the neutron flux distribution in the medium (let say in slab A), the albedo of the reflector can be used as a boundary condition for the diffusion equation solution. This boundary condition is similar to the vacuum boundary condition, i.e., Φ(Ralbedo) = 0, where Ralbedo = R + de and