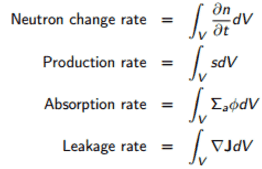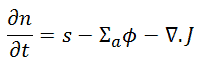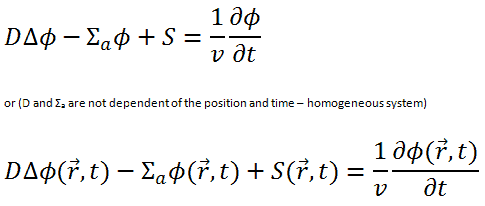The mathematical formulation of neutron diffusion theory is based on the balance of neutrons in a differential volume element. Since neutrons do not disappear (β decay is neglected), the following neutron balance must be valid in an arbitrary volume V.
rate of change of neutron density = production rate – absorption rate – leakage rate
where
Substituting for the different terms in the balanced equation and by dropping the integral over (because the volume V is arbitrary), we obtain:
where
- n is the density of neutrons,
- s is the rate at which neutrons are emitted from sources per cm3 (either from external sources (S) or from fission (ν.Σf.Ф)),
- J is the neutron current density vector
- Ф is the scalar neutron flux
- Σa is the macroscopic absorption cross-section
In steady state, when n is not a function of time:
The Diffusion Equation
In previous chapters, we introduced two bases for the derivation of the diffusion equation:
Fick’s law:
which states that neutrons diffuse from high concentration (high flux) to low concentration.
Continuity equation:
which states that rate of change of neutron density = production rate – absorption rate – leakage rate.
We return now to the neutron balance equation and substitute the neutron current density vector by J = -D∇Ф. Assuming that ∇.∇ = ∇2 = Δ (therefore div J = -D div (∇Ф) = -DΔФ) we obtain the diffusion equation.