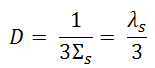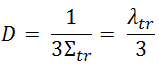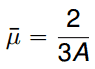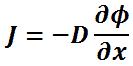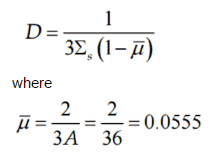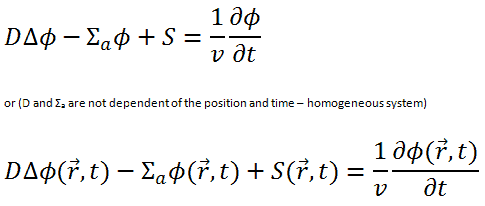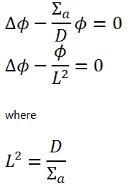From diffusion theory, the diffusion coefficient is expressed in terms of the macroscopic cross-section and mean free path as:
where Σs is the macroscopic scattering cross-section and λs is the scattering mean free path.
However, we can express the diffusion coefficient from the more advanced transport theory in terms of transport and absorption cross-sections:
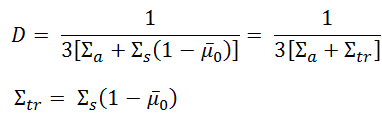
where:
- λtr is the transport mean free path
- Σa is the macroscopic absorption cross-section.
- Σtr is the macroscopic transport cross-section
- μ0 is the average value of the cosine of the angle in the lab system
In a weakly absorbing medium where Σa << Σs the diffusion coefficient can be approximately calculated as:
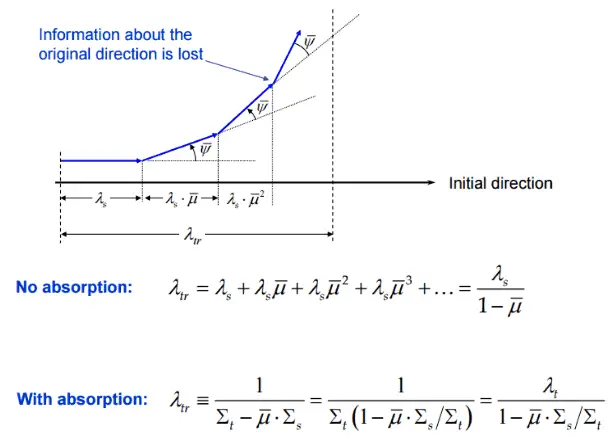
The transport means free path (λtr) is an average distance a neutron will move in its original direction after an infinite number of scattering collisions.
is the average value of the cosine of the angle in the lab system at which neutrons are scattered in the medium. It can be calculated for most of the neutron energies as (A is the mass number of target nucleus):
Physical Interpretation
where
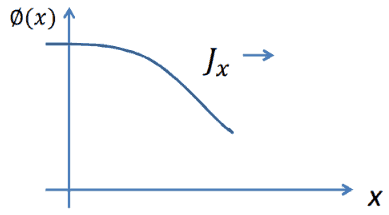
Consider neutrons passing through the plane at x=0 from left to right due to collisions to the left of the plane. Since the concentration of neutrons and the flux is larger for negative values of x, there are more collisions per cubic centimeter on the left. Therefore more neutrons are scattered from left to right, then the other way around. Thus the neutrons naturally diffuse toward the right. The diffusion coefficient determines the rate of diffusion.
Operational changes that affect the diffusion length
The diffusion coefficient is a very important parameter in thermal reactors, and its magnitude can be changed during reactor operation. Since the diffusion coefficient is dependent on the macroscopic scattering cross-section, Σs, we will study the impacts of operational changes on this parameter.
Change in the moderator temperature
The diffusion coefficient, D, is sensitive, especially on the change in the moderator temperature.
In short, as the moderator temperature increases, the diffusion coefficient also slightly increases.
This increase in the diffusion coefficient is especially due (Σs=σs.NH2O) to a decrease in the macroscopic scattering cross-section, Σs=σs.NH2O, caused by the thermal expansion of water (a decrease in the atomic number density).
Calculation of Diffusion Coefficient
The scattering cross-section of carbon at 1 eV is 4.8 b (4.8×10-24 cm2). Calculate the diffusion coefficient and the transport mean free path.
Solution:
We will calculate the diffusion according to the advanced formula:
First, we have to determine the atomic number density of carbon and then the scattering macroscopic cross-section.
Density:
MC = 12
NC = ρ . Na / MC
= (2.2 g/cm3)x(6.022×1023 nuclei/mol)/ (12 g/mol)
= 1.1×1023 nuclei / cm3
σs12C = 4.8 b
Σs12C = 4.8×10-24 x 1.1×1023 = 0.528 cm-1
the diffusion coefficient is then:
D = 1 / (3 x 0.528 x 0.9445) = 0.668 cm
the transport mean free path
λtr = 3 x D = 2.005 cm
Diffusion Coefficient and the Fick’s Law
The use of this law in nuclear reactor theory leads to the diffusion approximation.
Fick’s law in reactor theory stated that:
The current density vector J is proportional to the negative of the gradient of the neutron flux. The proportionality constant is called the diffusion coefficient and is denoted by the symbol D.
In one (spatial) dimension, the law is:
where:
- J is the neutron current density (neutrons.cm-2.s-1) along the x-direction, the net flow of neutrons that pass per unit of time through a unit area perpendicular to the x-direction.
- D is the diffusion coefficient, it has the unit of cm, and it is given by:
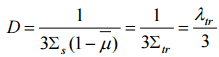
- φ is the neutron flux, the number of neutrons crossing through some arbitrary cross-sectional unit area in all directions per unit time.
The generalized Fick’s law (in three dimensions) is:
![]()
where J denotes the diffusion flux vector. Note that the gradient operator turns the neutron flux, a scalar quantity, into the neutron current, a vector quantity.
Diffusion Coefficient and the Diffusion Equation
The diffusion equation:
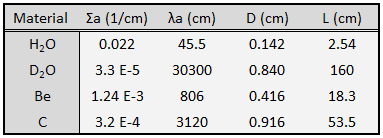
Diffusion Coefficient and Diffusion Length
During the diffusion equation solution, we often meet with a very important parameter that describes the behavior of neutrons in a medium.
The solution diffusion equation (let assume the simplest diffusion equation) usually starts by division of entire equation by diffusion coefficient:
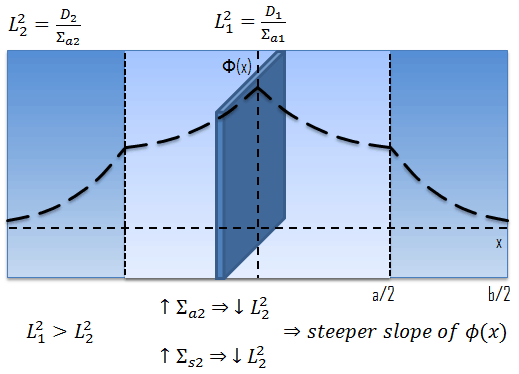
The term L2 is called the diffusion area (and L is called the diffusion length).