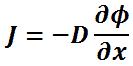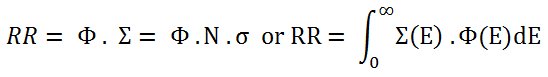Fick’s law in reactor theory states that:
The current density vector J is proportional to the negative of the gradient of the neutron flux. The proportionality constant is called the diffusion coefficient and is denoted by the symbol D.
In one (spatial) dimension, the law is:
In chemistry, Fick’s law states that:
Suppose the concentration of a solute in one region is greater than in another of a solution. In that case, the solute diffuses from the region of higher concentration to the region of lower concentration, with a magnitude that is proportional to the concentration gradient.
In one (spatial) dimension, the law is:
where:
- J is the diffusion flux,
- D is the diffusion coefficient,
- φ (for ideal mixtures) is the concentration.
The use of this law in nuclear reactor theory leads to the diffusion approximation.
Fick’s law in reactor theory states that:
The current density vector J is proportional to the negative of the gradient of the neutron flux. The proportionality constant is called the diffusion coefficient and is denoted by the symbol D.
In one (spatial) dimension, the law is:
where:
- J is the neutron current density (neutrons.cm-2.s-1) along the x-direction, the net flow of neutrons that pass per unit of time through a unit area perpendicular to the x-direction.
- D is the diffusion coefficient, it has the unit of cm, and it is given by:
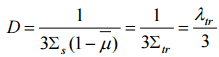
- φ is the neutron flux, the number of neutrons crossing through some arbitrary cross-sectional unit area in all directions per unit time.
The generalized Fick’s law (in three dimension) is:
where J denotes the diffusion flux vector. Note that the gradient operator turns the neutron flux, which is a scalar quantity into the neutron current, which is a vector quantity.
Physical Interpretation
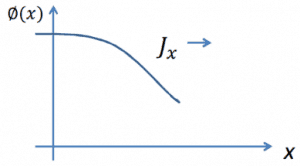The physical interpretation is similar to the fluxes of gases. The neutrons exhibit a net flow in the direction of least density. This is a natural consequence of greater collision densities at positions of greater neutron densities.
Consider neutrons passing through the plane at x=0 from left to right due to collisions to the left of the plane. Since the concentration of neutrons and the flux is larger for negative values of x, there are more collisions per cubic centimeter on the left. Therefore more neutrons are scattered from left to right, then the other way around. Thus the neutrons naturally diffuse toward the right.
Ф = n.v
where:
Ф – neutron flux (neutrons.cm-2.s-1)
n – neutron density (neutrons.cm-3)
v – neutron velocity (cm.s-1)
The neutron flux, the number of neutrons crossing through some arbitrary cross-sectional unit area in all directions per unit time, is a scalar quantity. Therefore it is also known as the scalar flux. The expression Ф(E).dE is the total distance traveled during one second by all neutrons with energies between E and dE located in 1 cm3.
The connection to the reaction rate, respectively, the reactor power is obvious. Knowledge of the neutron flux (the total path length of all the neutrons in a cubic centimeter in a second) and the macroscopic cross-sections (the probability of having an interaction per centimeter path length) allows us to compute the rate of interactions (e.g.,, rate of fission reactions). The reaction rate (the number of interactions taking place in that cubic centimeter in one second) is then given by multiplying them together:
where:
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross-section (cm2)
N – atomic number density (atoms.cm-3)
This flux of neutron flux is called the neutron current density. We have to distinguish between the neutron flux and the neutron current density. Although both physical quantities have the same units, namely, neutrons.cm-2.s-1, their physical interpretations are different. In contrast to the neutron flux, the neutron intensity is the number of neutrons crossing through some arbitrary cross-sectional unit area in a single direction per unit time (a surface is perpendicular to the direction of the beam). The neutron current density is a vector quantity.
The vector J is defined as the following integral:
A typical thermal reactor contains about 100 tons of uranium with an average enrichment of 2% (do not confuse it with the enrichment of the fresh fuel). If the reactor power is 3000MWth, determine the reaction rate and the average core thermal flux.
Solution:
Multiplying the reaction rate per unit volume (RR = Ф . Σ) by the total volume of the core (V) gives us the total number of reactions occurring in the reactor core per unit time. But we also know the amount of energy released per one fission reaction to be about 200 MeV/fission. Now, it is possible to determine the rate of energy release (power) due to the fission reaction. It is given by the following equation:
P = Ф . Σf . Er . V = Ф . NU235 . σf235 . Er . V
where:
P – reactor power (MeV.s-1)
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
Er – the average recoverable energy per fission (MeV / fission)
V – total volume of the core (m3)
The amount of fissile 235U per the volume of the reactor core.
m235 [g/core] = 100 [metric tons] x 0.02 [g of 235U / g of U] . 106 [g/metric ton] = 2 x 106 grams of 235U per the volume of the reactor core
The atomic number density of 235U in the volume of the reactor core:
N235 . V = m235 . NA / M235
= 2 x 106 [g 235 / core] x 6.022 x 1023 [atoms/mol] / 235 [g/mol]
= 5.13 x 1027 atoms / core
The microscopic fission cross-section of 235U (for thermal neutrons):
σf235 = 585 barns
The average recoverable energy per 235U fission:
Er = 200.7 MeV/fission
Validity of Fick’s Law
It must be emphasized that Fick’s law is an approximation and was derived under the following conditions:
- Infinite medium. This assumption is necessary to allow integration of overall space. Still, flux contributions are negligible beyond a few mean free paths (about three mean free paths) from the boundaries of the diffusive medium.
- Sources or sinks. Derivation of Fick’s law assumes that the contribution to the flux is mostly from elastic scattering reactions. Source neutrons contribute to the flux if they are more than a few mean free paths from a source.
- Uniform medium. Derivation of Fick’s law assumes that a uniform medium was used. There are different scattering properties at the boundary (interface) between the two media.
- Isotropic scattering. Isotropic scattering occurs at low energies but is not true in general. Anisotropic scattering can be corrected by modification of the diffusion coefficient (based on transport theory).
- Low absorbing medium. Fick’s law derivation assumes (an expansion in Taylor’s series) that the neutron flux, φ, is slowly varying. Large variations in φ occur when Σa (neutron absorption) is large (compared to Σs). Σa << Σs
- Time-independent flux. Derivation of Fick’s law assumes that the neutron flux is independent of time.
To some extent, these limitations are valid in every practical reactor. Nevertheless Fick’s law gives a reasonable approximation. For more detailed calculations, higher order methods are available.