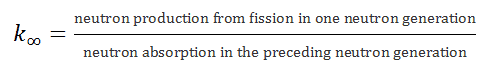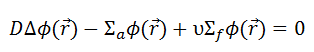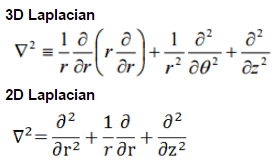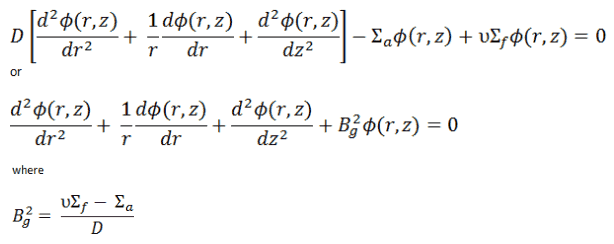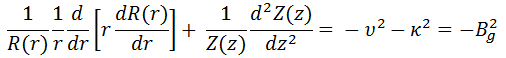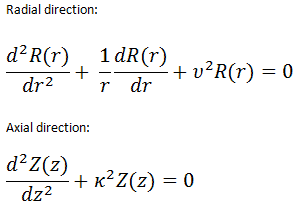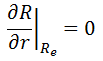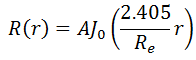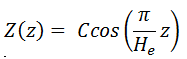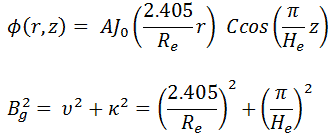Diffusion Equation – Finite Cylindrical Reactor

Solutions of the Diffusion Equation – Multiplying Systems

In previous section it has been considered that the environment is non-multiplying. In a non-multiplying environment, neutrons are emitted by a neutron source situated in the center of a coordinate system and then freely diffuse through media. We are now prepared to consider neutron diffusion in the multiplying system containing fissionable nuclei (i.e., Σ_f ≠ 0). In this multiplying system, we will also study the spatial distribution of neutrons, but in contrast to the non-multiplying environment, these neutrons can trigger nuclear fission reactions.

In this section, we will solve the following diffusion equation

in various geometries that satisfy the boundary conditions. In this equation ν is number of neutrons emitted in fission and  Σ_f is macroscopic cross-section of fission reaction. Ф denotes a reaction rate. For example a fission of ²³⁵U by thermal neutron yields 2.43 neutrons.

It must be noted that we will solve the diffusion equation without any external source. This is very important because such an equation is a linear homogeneous equation in the flux. Therefore if we find one solution of the equation, then any multiple is also a solution. This means that the absolute value of the neutron flux cannot possibly be deduced from the diffusion equation. This is totally different from problems with external sources, which determine the absolute value of the neutron flux.

We will start with simple systems (planar) and increase complexity gradually. The most important assumption is that all neutrons are lumped into a single energy group, they are emitted and diffuse at thermal energy (0.025 eV). Solutions of diffusion equations in this case provides an illustrative insights, how can be the neutron flux distributed in a reactor core.

Solution for the Finite Cylindrical Reactor

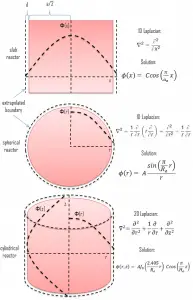
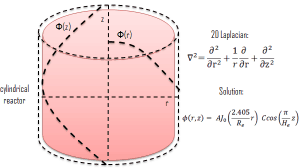Let assume a uniform reactor (multiplying system) in the shape of a cylinder of physical radius R and height H. This finite cylindrical reactor is situated in cylindrical geometry at the origin of coordinates. To solve the diffusion equation, we have to replace the Laplacian by its cylindrical form:

Since there is no dependence on angle Θ, we can replace the 3D Laplacian with its two-dimensional form and solve the problem in radial and axial directions. Since the flux is a function of radius – r and height – z only (Φ(r,z)), the diffusion equation can be written as:

The solution of this diffusion equation is based on the use of the separation-of-variables technique, therefore:

where R(r) and Z(z) are functions to be determined. Substituting this into the diffusion equation and dividing by R(r)Z(z), we obtain:

Because the first term depends only on r and the second only on z, both terms must be constants for the equation to have a solution. Suppose we take the constants to be v² and к. The sum of these constants must be equal to B_g² = v² + к². Now we can separate variables, and the neutron flux must satisfy the following differential equations:

Solution for the radial direction

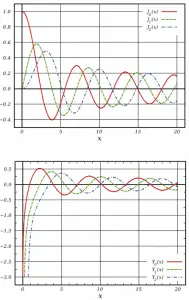The differential equation for radial direction is called Bessel’s equation, and it is well known to mathematicians. In this case, the Bessel’s equation’s solutions are called the Bessel functions of the first and second kind, J_α(x) and Y_α(x), respectively.

For r > 0, this differential equation has two possible solutions, J₀(vr) and Y₀(vr), the Bessel functions of order zero, which give a general solution:

From finite flux condition (0≤ Φ(r) < ∞), which required only reasonable values for the flux, it can be derived that C must be equal to zero. The term Y₀(vr) goes to -∞ as r ➝0  and therefore cannot be part of a physically acceptable solution. The physically acceptable solution must then be:

R(r) =  AJ₀(vr)

The vacuum boundary condition requires the relative neutron flux near the boundary to have a slope of -1/d, i.e., the flux would extrapolate linearly to 0 at a distance d beyond the boundary. This zero flux boundary condition is more straightforward, and it can be written mathematically as:

If d is not negligible, physical dimensions of the reactor are increased by d, and extrapolated boundary is formulated with dimension R_e = R + d, and this condition can be written as Φ(R + d) =  Φ(R_e) = 0.

Therefore, the solution must be  R(R_e) =  A J₀(vR_e) = 0. The function of J₀(r) has several zeroes. The first is at r₁ = 2.405, and the second at r₂ = 5.6. However, because the neutron flux cannot have regions of negative values, the only physically acceptable value for v is 2.405/R_e. The solution of the diffusion equation is:

Solution for axial direction

The solution for axial direction has been solved in previous sections (Infinite Slab Reactor), and therefore it has the same solution. The solution in an axial direction is:

Solution for radial and axial directions

The full solution for the neutron flux distribution in the finite cylindrical reactor is, therefore:

where B_g² is the total geometrical buckling.

The constants A and C must be added that they cannot be obtained from the diffusion equation because they give the absolute value of neutron flux. The neutron flux can have any value, and the critical reactor can operate at any power level. It should be noted this flux shape is only in a hypothetical case in a uniform homogeneous cylindrical reactor at low power levels (at “zero power criticality”).

In a power reactor core, the neutron flux can reach, for example, about 3.11 x 10¹³ neutrons.cm^-2.s^-1, but these values depend significantly on many parameters (type of fuel, fuel burnup, fuel enrichment, position in fuel pattern, etc.).

The power level does not influence the criticality (k_eff) of a power reactor unless thermal reactivity feedbacks act (operation of a power reactor without reactivity feedbacks is between 10E-8% – 1% of rated power).

 

See above:

Diffusion Theory