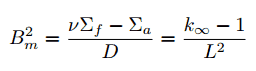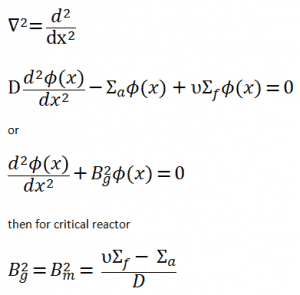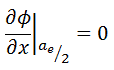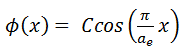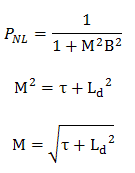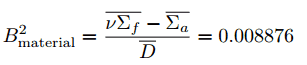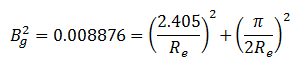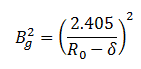Material Buckling
In earlier text, the term Bm first appeared in the following equation:
This parameter is known as the material buckling, and it describes the characteristics of the fuel material in an infinite medium. For example, assume a uniform reactor (multiplying system) in the shape of a slab of physical width a in the x-direction and infinite in the y- and z-directions. This reactor is situated in the center at x=0. In this geometry, the flux does not vary in y and z allowing us to eliminate the y and z derivatives from ∇2. The flux is then a function of x only, and therefore the Laplacian and diffusion equation can be written as:
Geometrical Buckling
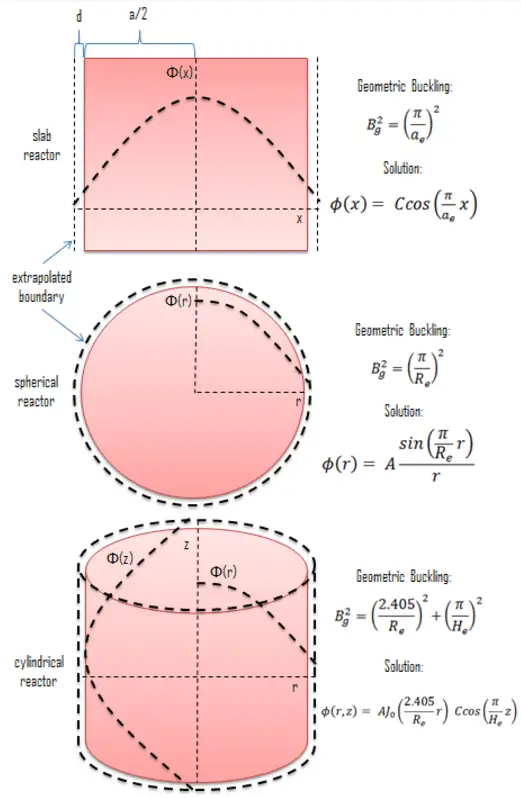
Geometrical buckling is a measure of neutron leakage, while material buckling is a measure of neutron production minus absorption. With this terminology, the criticality condition may also be stated as the material and geometric buckling being equal:
Bm = Bg
The quantity Bg2 is called the geometrical buckling of the reactor and depends only on the geometry. This term is derived from the notion that the neutron flux distribution is somehow ‘‘buckled’’ in a homogeneous finite reactor. It can be derived the geometrical buckling is the negative relative curvature of the neutron flux (Bg2 = ∇2Ф(x) / Ф(x)). The neutron flux has more concave downward or ‘‘buckled’’ curvature (higher Bg2) in a small reactor than in a large one.
The value of geometrical buckling for an infinite slab reactor can be derived when the vacuum boundary condition is applied to the diffusion equation solution. The physically acceptable solution for an infinite slab reactor is:
Φ(x) = C.cos(Bg x)
The vacuum boundary condition requires the relative neutron flux near the boundary to have a slope of -1/d, i.e., the flux would extrapolate linearly to 0 at a distance d beyond the boundary. This zero flux boundary condition is more straightforward, and it can be written mathematically as:
Therefore, the solution must be Φ(ae/2) = C.cos(Bg .ae/2) = 0 and the values of geometrical buckling, Bg, are limited to Bg = nπ/a_e, where n is any odd integer. The only one physically acceptable odd integer is n=1 because higher values of n would give cosine functions which would become negative for some values of x. The solution of the diffusion equation is:
Criticality Condition
The basic classification of states of a reactor is according to the multiplication factor as eigenvalue, which measures the change in the fission neutron population from one neutron generation to the subsequent generation.
- keff < 1. This condition is known as the subcritical state.
- keff = 1. This condition is known as the critical state.
- keff > 1. This condition is known as the supercritical state.
But these three basic states may also be defined according to the material and geometrical bucklings:
- Bm < Bg. When a reactor is smaller (i.e., higher Bg and higher relative curvature) than the critical size for a given material, Bm < Bg, the reactor is subcritical.
- Bm = Bg. When a reactor size matches the critical size for a given material, Bm = Bg, then the reactor is critical.
- Bm > Bg. When a reactor is larger than the critical size for a given material, Bm > Bg, then the reactor is supercritical.
It must be added, and for any positive value of materials buckling, there is a unique critical size for each reactor geometry. For reactors of shapes other than spheres, the geometrical buckling takes the form Bg = C/R, where the coefficient C is determined by the solution of the diffusion equation with vacuum boundary condition. R is a characteristic dimension. Generally, the multiplication of a uniform reactor of any shape and size is given by keff = k∞.PNL, with the non/leakage probability written as (for large reactors):
where M2 is the migration area, and the subscript is dropped from B, the geometric buckling. As can be seen, the total non-leakage probability of large reactors is primarily a function of migration area and the relative curvature of the neutron flux given by the geometrical buckling.
Example: Calculate the geometrical buckling
Let assume a bare square cylinder (i.e., height = diameter; H = 2R). Assume that the material buckling of this reactor, which is given using one-group cross-sections, is:
Calculate the critical radius (Bm = Bg) using the one-group diffusion theory.
The geometrical buckling with extrapolated distance is:
From this equation, we can get Re= 30.5 cm.
Geometric Buckling of Reflected Reactor
Adding a reflector to a reactor allows either the volume of the reactor or the requirements on fuel to be reduced or some combination of the two. If the reflector savings is known, the calculation of the critical dimensions of a reflected reactor needs only the solution of the bare reactor, which is a simpler problem. For example, it is only necessary for the cylindrical reactor to determine the bare critical radius R0 and the reflected radius is simply R = R0 – δ, where R0 is the critical diameter of a bare reactor. The geometrical buckling of infinite cylindrical reactor will then be: