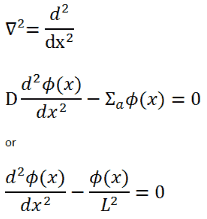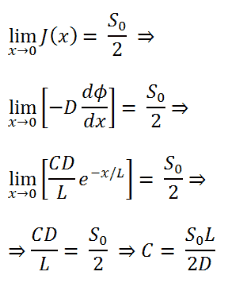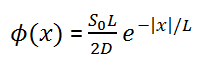Solutions of the Diffusion Equation – Non-multiplying Systems
in various geometries that satisfy the boundary conditions discussed in the previous section.
We will start with simple systems and increase complexity gradually. The most important assumption is that all neutrons are lumped into a single energy group. They are emitted and diffuse at thermal energy (0.025 eV).
In the first section, we will deal with neutron diffusion in a non-multiplying system, i.e., in a system where fissile isotopes are missing, the fission cross-section is zero. The neutrons are emitted by an external neutron source. We will assume that the system is uniform outside the source, i.e., D and Σa are constants.
Solution for the Infinite Planar Source
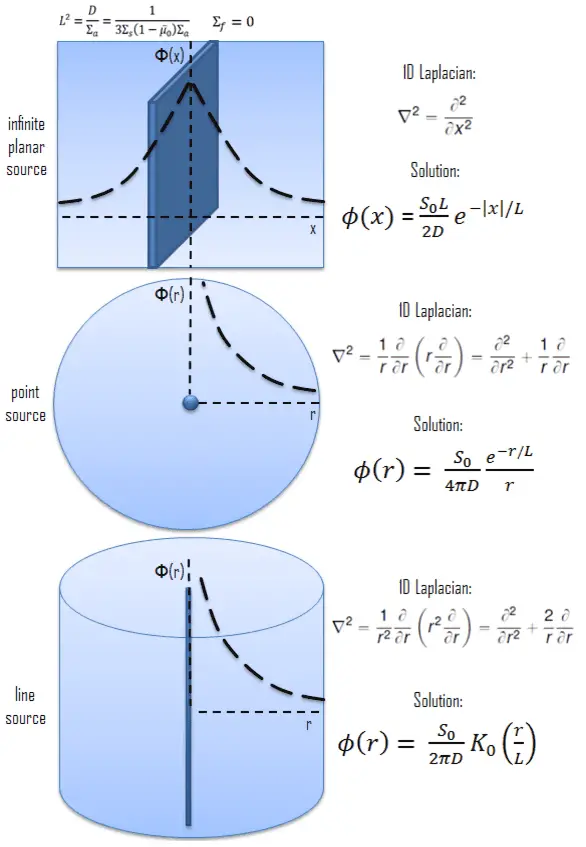
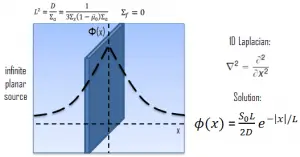Let us assume the neutron source (with strength S0) as an infinite plane source (in y-z plane geometry). In this geometry, the flux varies slowly in y and z allowing us to eliminate the y and z derivatives from ∇2. The flux is then a function of x only, and therefore the Laplacian and diffusion equation (outside the source) can be written as (everywhere except x = 0):
For x > 0, this diffusion equation has two possible solutions exp(x/L) and exp(-x/L), which give a general solution:
Φ(x) = Aexp(x/L) + Cexp(-x/L)
Note that B is not usually used as a constant because B is reserved for a buckling parameter. To determine the coefficients A and C, we must apply boundary conditions.
From finite flux condition (0≤ Φ(x) < ∞), which required only reasonable values for the flux, it can be derived that A must be equal to zero. The term exp(x/L) goes to ∞ as x ➝∞ and therefore cannot be part of a physically acceptable solution for x > 0. The physically acceptable solution for x > 0 must then be:
Φ(x) = Ce-x/L
where C is a constant that can be determined from the source condition at x ➝0.
If S0 is the plane’s source strength per unit area, then the number of neutrons crossing outwards per unit area in the positive x-direction must tend to S0 /2 as x ➝0.
So that the solution may be written:
