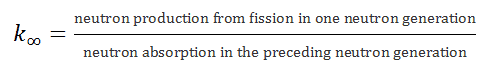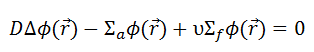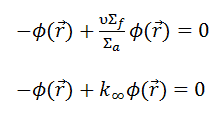Diffusion Equation - Infinite Reactor

Solutions of the Diffusion Equation – Multiplying Systems

In previous section it has been considered that the environment is non-multiplying. In a non-multiplying environment, neutrons are emitted by a neutron source situated in the center of a coordinate system and then freely diffuse through media. We are now prepared to consider neutron diffusion in the multiplying system containing fissionable nuclei (i.e., Σ_f≠ 0). In this multiplying system, we will also study the spatial distribution of neutrons, but in contrast to the non-multiplying environment, these neutrons can trigger nuclear fission reactions.

Multiplying systems from criticality point of view

The required condition for a stable, self-sustained fission chain reaction in a multiplying system (in a nuclear reactor) is that exactly every fission initiate another fission. The minimum condition is for each nucleus undergoing fission to produce, on average, at least one neutron that causes fission of another nucleus. Also, the number of fissions occurring per unit time (the reaction rate) within the system must be constant.

This condition can be expressed conveniently in terms of the multiplication factor. The infinite multiplication factor is the ratio of the neutrons produced by fission in one neutron generation to the number of neutrons lost through absorption in the preceding neutron generation. This can be mathematically expressed as shown below.

The infinite multiplication factor in a multiplying system measures the change in the fission neutron population from one neutron generation to the subsequent generation.

k_∞ < 1. Suppose the multiplication factor for a multiplying system is less than 1.0. In that case, the number of neutrons decreases in time (with the mean generation time), and the chain reaction will never be self-sustaining. This condition is known as the subcritical state.

k_∞ = 1. If the multiplication factor for a multiplying system is equal to 1.0, then there is no change in neutron population in time, and the chain reaction will be self-sustaining. This condition is known as the critical state.

k_∞ > 1. If the multiplication factor for a multiplying system is greater than 1.0, then the multiplying system produces more neutrons than are needed to be self-sustaining. The number of neutrons is exponentially increasing in time (with the mean generation time). This condition is known as the supercritical state.

Reactor criticality. A – a supercritical state; B – a critical state; C – a subcritical state

In this section, we will solve the following diffusion equation

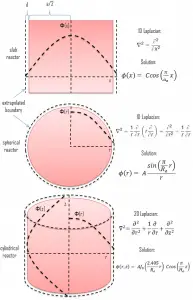
in various geometries that satisfy the boundary conditions. In this equation ν is number of neutrons emitted in fission and Σ_f is macroscopic cross-section of fission reaction. Ф denotes a reaction rate. For example a fission of ²³⁵U by thermal neutron yields 2.43 neutrons.

It must be noted that we will solve the diffusion equation without any external source. This is very important because such an equation is a linear homogeneous equation in the flux. Therefore if we find one solution of the equation, then any multiple is also a solution. This means that the absolute value of the neutron flux cannot possibly be deduced from the diffusion equation. This is totally different from problems with external sources, which determine the absolute value of the neutron flux.

We will start with simple systems (planar) and increase complexity gradually. The most important assumption is that all neutrons are lumped into a single energy group, they are emitted and diffuse at thermal energy (0.025 eV). Solutions of diffusion equations in this case provides an illustrative insights, how can be the neutron flux distributed in a reactor core.

Solution for the Infinite Reactor

Let assume a uniform infinite reactor, i.e., a uniform infinite multiplying system without an external neutron source. This system is in a Cartesian coordinate system, and under these assumptions (no neutron leakage, no changes in diffusion parameters), the neutron flux must be inherently constant throughout space.

Since the neutron current is equal to zero (J = -D∇Ф, where Ф is constant), the diffusion equation in the infinite uniform multiplying system must be:

The only solution of this equation is a trivial solution, i.e., Ф = 0, unless Σ_a = νΣ_f. This equation (Σ_a = νΣ_f) is the criticality condition for an infinite reactor and expresses the perfect balance (critical state) between neutron absorption and neutron production. This balance must be continuously maintained to have a steady-state neutron flux.

Infinite Multiplication Factor

In this section, the infinite multiplication factor, k_∞, will be defined from another point of view than in section – Nuclear Chain Reaction.

As can be seen, we can rewrite the diffusion equation in the following way, and we can define a new factor – k_∞ = νΣ_f/ Σ_a:

A non-trivial solution of this equation is guaranteed when k_∞ = νΣ_f/ Σ_a= 1. On the other hand, we have no information about the neutron flux in such a critical reactor. The neutron flux can have any value, and the critical uniform infinite reactor can operate at any power level. It should be noted this theory can be used for a reactor at low power levels, hence “zero power criticality”.

In a power reactor core, the power level does not influence the criticality of a reactor unless thermal reactivity feedbacks act (operation of a power reactor without reactivity feedbacks is between 10E-8% – 1% of rated power).

See above:

Diffusion Theory