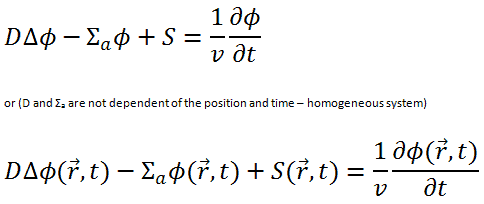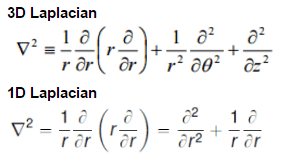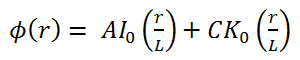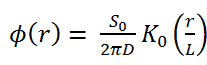Diffusion Equation – Line Source

Solutions of the Diffusion Equation – Non-multiplying Systems

As was previously discussed the diffusion theory is widely used in core design of the current Pressurized Water Reactors (PWRs) or Boiling Water Reactors (BWRs). This section is not about such calculations but provides illustrative insights, how can be the neutron flux distributed in any diffusion medium. In this section, we will solve diffusion equations:

in various geometries that satisfy the boundary conditions discussed in the previous section.

We will start with simple systems and increase complexity gradually. The most important assumption is that all neutrons are lumped into a single energy group. They are emitted and diffuse at thermal energy (0.025 eV).

In the first section, we will deal with neutron diffusion in a non-multiplying system, i.e., in a system where fissile isotopes are missing, the fission cross-section is zero. The neutrons are emitted by an external neutron source. We will assume that the system is uniform outside the source, i.e., D and Σ_a are constants.

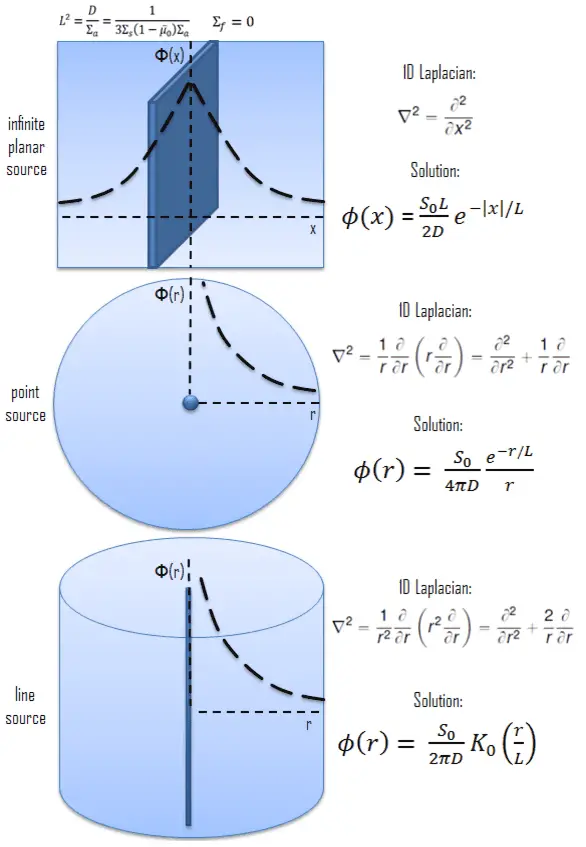
Solution for the Line Source

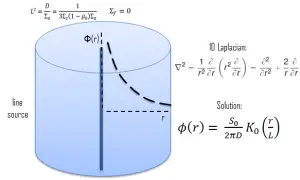The neutron source (with strength S₀) is an isotropic line source situated in an infinite cylindrical geometry. This line source is placed at r = 0. To solve the diffusion equation, we have to replace the Laplacian by its cylindrical form:

Since there is no dependence on angle Θ and z-coordinate, we can replace the 3D Laplacian with its one-dimensional form and solve the problem only in the radial direction. The source is assumed to be an isotropic source. Since the flux is a function of radius – r only, the diffusion equation (outside the source) can be written as (everywhere except r = 0):

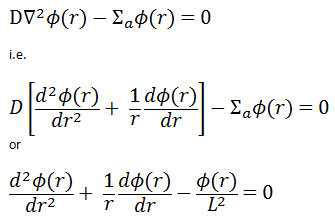
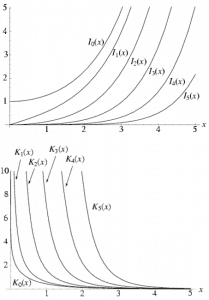This differential equation is called Bessel’s equation, and it is well known to mathematicians. In this case, the solutions to the Bessel’s equation are called the modified Bessel functions (or occasionally the hyperbolic Bessel functions) of the first and second kind, I_α(x) and K_α(x), respectively.

For r > 0, this differential equation has two possible solutions, I₀(r/L) and K₀(r/L), the modified Bessel functions of order zero, which give a general solution:

To find constants A and C, we use the identical procedure as in the case of the infinite planar source. From finite flux condition (0≤ Φ(r) < ∞), which required only reasonable values for the flux, it can be derived that A must be equal to zero. The term I₀(r/L) goes to ∞ as r ➝∞  and therefore cannot be part of a physically acceptable solution for r > 0. The physically acceptable solution for r > 0 must then be:

Φ(r) =  C.K₀(r/L)

where C is a constant that can be determined from the source condition at r ➝0.

If S₀ is the source strength, then the number of neutrons crossing a cylinder outwards in the positive r-direction must tend to S₀ as r ➝0.

So that the solution may be written:

 

See above:

Diffusion Theory