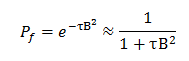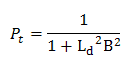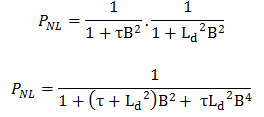Migration Length - Migration Area | Definition

Let us define the quantity, M², where:

M² = L² + L_s² or M² = L² + τ_th

This quantity is called the migration area or square of the migration length. The physical meaning of the migration area is:

M² is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a fast neutron) and its absorption (as a thermal neutron).

In general, the distribution of neutrons within a finite or infinite medium is determined by:

The source distribution, whether it is an external source of neutrons or is a multiplying environment.
The geometry (in a finite medium).
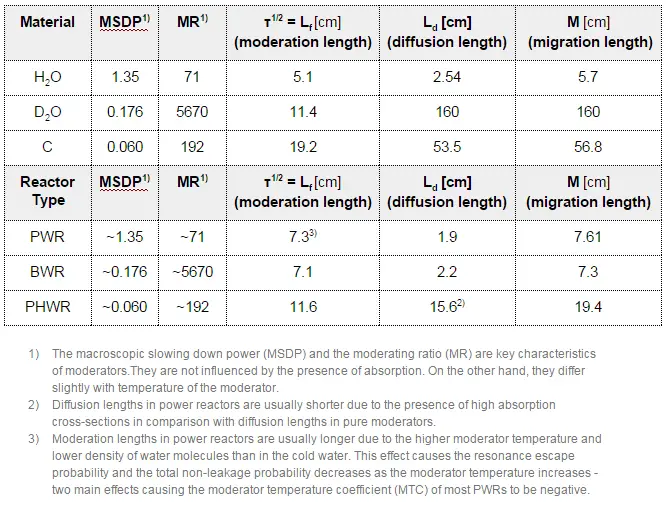
The neutron diffusion length, L² = D/Σ_a L^2, is the diffusion area. It is proportional to the distance thermal neutrons travel before they are absorbed.
The slowing-down length, L_s, of a neutron. It is proportional to the distance fast neutrons travel from when they are born to the point where they become thermalized. Since it can be derived from Fermi age theory, a parameter τ, called the “age” (often called the “Fermi age”), is often used.

Let us focus on the diffusion length and the slowing-down length.

The physical meaning of the diffusion length is that:

L² is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a thermal neutron) and its absorption.

The Fermi age is related to the distance traveled during moderation, just as the diffusion length is for thermal neutrons. The Fermi age is the same quantity as the slowing-down length squared, L_s², but the slowing-down length is the square root of the Fermi age, τ_th= L_s². The physical meaning of the slowing-down length is:

L_s² is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a fast neutron) and the point where it has become thermalized.

Let us define the quantity, M², where:

M² = L² + L_s² or M² = L² + τ_th

This quantity is called the migration area or square of the migration length. The physical meaning of the migration area is:

M² is equal to one-sixth of the square of the average distance (in all dimensions) between the neutron’s birth point (as a fast neutron) and its absorption (as a thermal neutron).

The distance traveled by fast neutrons during moderation and the distance traveled by thermal neutrons during diffusion in a reactor is important to reactor design because of their effect on the critical size and their effect on the neutron leakage.

Effect on the Neutron Leakage

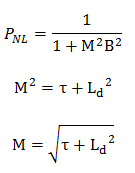It can be derived the total non-leakage probability of large reactors is primarily a function of migration area.

Fast Non-leakage Probability

It can be derived from the Fermi age theory, the probability that a neutron will remain in the core and become a thermal neutron without being lost by fast leakage is also represented by the following equation:

where τ is the Fermi age of the neutron, B is the geometrical buckling (in case of critical state B_g = B_m), which depends only on the shape and size of the core. The value of B for small cores is higher than the value for large cores. So that, it is obvious, the fast neutrons leakage is higher for small cores and depends on the macroscopic slowing down the power of neutron moderator (leakage is higher for poor moderators).

Thermal Non-leakage Probability

It can be derived from the neutron diffusion theory. The probability that a thermal neutron will remain in the core is also represented by the following equation:

L_d is the diffusion length, B is the geometrical buckling (in case of critical state B_g = B_m), which depends only on the shape and size of the core. The value of B for small cores is higher than the value for large cores.

Total Non-leakage Probability

The fast non-leakage probability (P_f) and the thermal non-leakage probability (P_t) may be combined into one term that gives the fraction of all neutrons that do not leak out of the reactor core. This term is called the total non-leakage probability and is given the symbol P_NL, and may be expressed by the following equation:

We can rewrite this equation without a substantial loss of accuracy for large reactors simply by replacing the diffusion length L_d and the fermi age τ with the migration length M in the one group equation. The term B⁴ is very small for large reactors, and therefore it can be neglected. We may then write.

where M is the migration area (m²), the migration length is defined as the square root of the migration area. As can be seen, the total non-leakage probability of large reactors is primarily a function of the migration area.

Main operational changes, that affect the neutron leakage

Since both (P_f and P_t) are affected by a change in moderator temperature in a heterogeneous water-moderated reactor, and the directions of the feedbacks are the same, the resulting total non-leakage probability is also sensitive on the change in the moderator temperature. As a result, an increase in the moderator temperature causes that the probability of leakage to increase. This effect is one of two main effects causing the moderator temperature coefficient (MTC) of most PWRs to be negative.

The thermal neutron leakage is dependent on the core temperature (or moderator temperature). The moderator temperature influences macroscopic cross-sections for elastic scattering reaction, especially the atomic number density – N_H2O(Σ_s=σ_s.N_H₂O) due to the thermal expansion of water. Also, the microscopic cross-section (σ_a) for neutron absorption changes with core temperature. Both processes have the same direction. As the temperature of the core increases, the diffusion coefficient (D = 1/3.Σ_tr) increases, and the absorption cross-section decreases, which causes the increase in the thermal neutron leakage. This physical process is a part of the moderator temperature coefficient (MTC).

The fast neutron leakage is also dependent on the core temperature (or moderator temperature). The moderator temperature influences macroscopic cross-sections for elastic scattering reaction (Σ_s=σ_s.N_H₂O) due to the thermal expansion of water. As the temperature of the core increases, the fast neutron leakage increases. This physical process is a part of the moderator temperature coefficient (MTC). It is responsible for an increase in neutron flux measured by neutron detectors situated around the reactor vessel.

In power reactors, the total non-leakage probability also significantly changes with fuel burnup. This dependency is not associated with any of the parameters like the diffusion coefficient or the geometrical buckling. In power reactors, the total non-leakage probability strongly depends on the certain fuel loading pattern, and the reload strategy. Neutron leakage is one of the key parameters in the neutron and fuel economy.

To enhance the neutron and fuel economy, core designers design the low leakage loading patterns, in which fresh fuel assemblies are not situated in the peripheral positions of the reactor core. The peripheral positions are loaded with the fuel with the highest fuel burnup. Compared to the average assemblies, these “high” burnup assemblies have inherently lower relative power (due to the lower k_inf and the fact they feel the presence of a non-multiplying environment). In short, this parameter is significantly dependent on a certain loading pattern. During fuel burnup, the neutron leakage usually increases, especially in low leakage loading patterns. This process is caused by reducing the differences in k_inf between fresh fuel assemblies and peripheral high-burnup assemblies.

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Diffusion Theory