The design and safe operation of nuclear reactors is based on detailed and accurate knowledge of the spatial and temporal behavior of the core power distribution everywhere within the core. This knowledge is necessary to ensure that:
- the reactor can be safely operated at certain power
- the power density in localized regions does not exceed the limits of fuel integrity
- the fission chain reaction can be quickly shutdown
- the power plant is prepared to withstand all anticipated transients, which are of importance in reactor safety and in must be proved and declared in the Safety Analysis Report (SAR)
Nowadays, reactor core analyses and designs are often performed using nodal two-group diffusion methods. These methods are based on pre-computed assembly homogenized cross-sections, diffusion coefficients, and assembly discontinuity factors (pin factors) obtained by single assembly calculation with reflective boundary conditions (infinite lattice). Highly absorbing control elements are represented by effective diffusion theory cross-sections, which reproduce transport theory absorption rates. These pre-computed data (discontinuity factors, homogenized cross-sections, etc.) are calculated by neutron transport codes based on a more accurate neutron transport theory. In short, neutron transport theory is used to make diffusion theory work. The neutron transport equation is the most fundamental and exact description of the distribution of neutrons in space, energy, and direction (of motion). It is the starting point for approximate methods.
Two methods exist for the calculation of the pre-computed assembly cross-sections and pin factors.
- Deterministic methods that solve the Boltzmann transport equation.
- Stochastic methods are known as Monte Carlo methods that model the problem almost exactly.
The diffusion equation can be derived by adding an additional assumption that the angular flux has a linearly anisotropic directional dependence in isotropic sources and scattering problems. This allows the removal of the directional variables from the neutron density and simplifies the governing equation and associated numerical methods.
In common practice, these methods can be divided into two classes based on the relative spatial mesh size over which the numerical approximations are valid.
- In reactor applications, finite difference methods are generally restricted to very small spatial meshes (fine mesh method) — typically about 1cm.
- Nodal methods are based on a higher-order (or even analytical) expansion of the solution in the spatial variable. They are applied to meshes much larger (coarse-mesh method) than a mean free path.
Nodal Method in Neutron Diffusion
The steady-state core analysis of both new reactor designs and the reload cores of operating reactors involves many whole-core calculations to optimize loading patterns and determine to reload safety parameters. It must be noted that:
- There are about 60 000 fuel pins in a reactor core. These fuel pins must be divided into about 50 axial levels (axial nodalization) to evaluate thermal margins. At one state point, coupling of neutronics/fuel heat conduction/coolant hydraulics/structural mechanics is needed to evaluate thermal margins.
- Each fuel cycle has to be analyzed for about tens of states (fuel burnup), and about 300 isotopes must be tracked.
- Millions of cycle depletion simulations have to be performed for designing loading design and optimization.
- Hundreds of startup and maneuver simulations have to be performed.
- Hundreds of transient accident simulations have to be performed for safety analysis.
As a result, at the current speed of computational machinery, it is absolutely impractical to perform all of these calculations by applying fine-mesh transport methods to a model containing detail at the level of individual fuel rods, control elements, and coolant regions in an entire reactor core.
Reference: Scott W. Mosher, A Variational Transport Theory Method for Two-Dimensional Reactor Core Calculations. Georgia Institute of Technology, 2004.
For this reason, nodal methods are currently widely used to predict the neutronic behavior of a reactor core. In general nodal methods are based on a multi-phase approach:
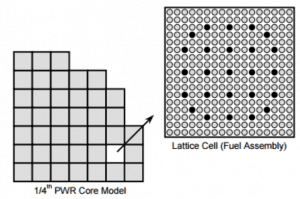Lattice Cell Homogenization. In the first phase, the reactor core is decomposed into relatively small core sub-regions, called lattice cells. A lattice cell typically contains a single fuel assembly plus half of the surrounding coolant gap. It is precisely modeled in two-dimensional geometry with materials characterized by fine-group cross-sections (100s of energy group). The reflective boundary condition (infinite lattice) is used. It is equivalent to a problem involving an infinitely large core composed of a single type of assembly. These calculations are performed by two-dimensional neutron transport codes based on a more accurate neutron transport theory. The neutron flux distribution from these fine-mesh calculations is used to spatially homogenize and condense (with respect to energy) cross-sections and to calculate pin power factors. In this phase, self-shielding corrections are applied to the flux distribution. The homogenized lattice cell data are then used in a simplified core model to which less expensive diffusion theory is applied in the second phase, the nodal calculations.- Nodal Calculations. A homogenized lattice cell (one single node) is typically represented by a 20 cm high section of a single fuel assembly. The nodal approach involves a high-order or analytical expansion of the intra-nodal flux shape to achieve a higher degree of accuracy, for a given node size, than the conventional finite difference approach to discretizing the spatial variable. The nodal balance equation is solved within each node, derived from the 3D steady-state multigroup neutron diffusion equation and the nodal balance equation.
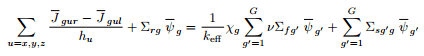There is a set of equations for the surface average currents instead of directly solving 3D finite difference equations. In approaching surface averaged current, the average flux derivative on a surface is approximated as the derivative of average flux at the surface. It is more efficient to work with the diffusion equation for average flux than the diffusion equation for 3D point-wise fluxes. A transverse integration procedure is often employed to reduce the multi-dimensional equations to a set of coupled one-dimensional equations. The resulting system is then solved on a three-dimensional core model consisting of homogeneous nodes characterized by the generalized equivalence theory (GET) constants generated in the first phase. 
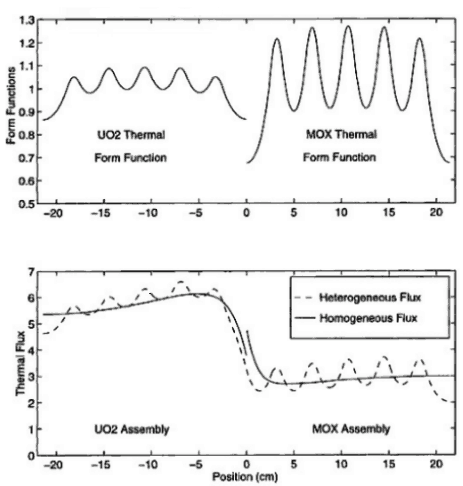Flux Reconstruction. In this phase, it is necessary to predict the neutron flux in individual fuel rods (pin-by-pin). Therefore we need the heterogeneous solution. The heterogeneous solution is reconstructed from a given homogenized solution. The detailed or heterogeneous flux distribution can be approximated by modulating the smooth nodal solution with the fine-mesh transport solutions using various techniques. The figure shows a superposition of lattice flux (form functions) determined by fine-mesh transport codes with nodal fluxes determined by nodal calculations.
The efficiency of nodal methods is very high and comparable with the finite difference methods. It is very fast and allows us to compute such a huge number of reactor states. It must be added, using this method, one can get only approximate information about the neutron flux in a single node (or coarse-mesh area, usually a single fuel assembly of a 20 cm height). This analysis requires many subsequent calculations of the flux and power distributions for the fuel assemblies while there is no need for detailed distribution within the assembly. For obtaining detailed distribution within the assembly, the heterogeneous flux reconstruction must be applied. However, homogenization of fuel assembly properties, required for the nodal method, may cause difficulties when applied to fuel assemblies with many burnable absorber rods due to a very high absorption cross-section (especially with Gd – burnable absorbers) and very strong heterogeneity within the assembly.
These methods are very efficient and accurate when applied to the current Pressurized Water Reactors (PWRs) or Boiling Water Reactors (BWRs).
Core Design and Nuclear Calculations
Core design calculations are a challenging reactor engineering discipline. Such calculations are reactor-specific, and therefore they cannot be transferred from one power plant to another (especially if they have different reactor types). The fuel requirements cannot be based on estimations because the core design has too many variables and restrictions. The nuclear calculations consist of the following aspects:
- A mid-term analysis of reloading strategy
- Proposal of a reference loading pattern
- Reload safety evaluation of proposed loading pattern
A mid-term analysis of reloading strategy comprises calculations of the fuel requirements for several reloads in a row using simple nuclear codes based on point kinetics and linear reactivity model. This analysis aims to optimize a number of fresh fuel assemblies, their enrichment, and neutron leakage from the reactor core during several years (Mid-term analysis).
The proposal of a reference loading pattern or transition to a new fuel strategy is based on searching the loading patterns using 3D computational codes. Such outputs are crucial in respect of entire nuclear calculations. They provide detailed knowledge about the behavior of the reactor core during the fuel cycle. The output consists of the proposed fuel loading pattern, which must meet energy (cycle length on full power) and all safety requirements such as power distribution, peaking factors, reactivity feedbacks. These calculations can be extended by a cycle optimization, especially meaning searching the low leakage loading patterns with enhanced neutron and fuel economy.
Each change in the project or operation of nuclear power plant requires safety assessment, let alone such a significant change as is the switching of the fuel cycle strategy. The type of the particular safety assessment always depends on the nature of the change. Such calculations are then absolutely crucial for the whole middle part of the fuel cycle. In general, it must be proven that the new fuel strategy meets all safety criteria from the Safety Analysis Report (SAR). These criteria are divided into three areas:
- Neutron-physical criteria
- Thermal-hydraulic criteria
- Fuel rod criteria
