The steady-state core analysis of both new reactor designs and the reload cores of operating reactors involves many whole-core calculations to optimize loading patterns and determine to reload safety parameters. It must be noted that:
- There are about 60 000 fuel pins in a reactor core. These fuel pins have to be divided into about 50 axial levels (axial nodalization) to evaluate thermal margins. At one state point, coupling of neutronics/fuel heat conduction/coolant hydraulics/structural mechanics is needed to evaluate thermal margins.
- Each fuel cycle has to be analyzed for about tens of states (fuel burnup), and about 300 isotopes must be tracked.
- Millions of cycle depletion simulations have to be performed for designing loading design and optimization.
- Hundreds of startup and maneuver simulations have to be performed.
- Hundreds of transient accident simulations have to be performed for safety analysis.
As a result, at the current speed of computational machinery, it is impractical to perform all of these calculations by applying fine-mesh transport methods to a model containing detail at the level of individual fuel rods, control elements, and coolant regions in an entire reactor core.
Reference: Scott W. Mosher, A Variational Transport Theory Method for Two-Dimensional Reactor Core Calculations. Georgia Institute of Technology, 2004.
For this reason, nodal methods are currently widely used to predict the neutronic behavior of a reactor core. In general nodal methods are based on a multi-phase approach:
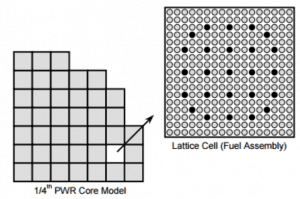 Lattice Cell Homogenization. In the first phase, the reactor core is decomposed into relatively small core sub-regions, called lattice cells. A lattice cell typically contains a single fuel assembly plus half of the surrounding coolant gap. It is precisely modeled in two-dimensional geometry with materials characterized by fine-group cross-sections (100s of energy group). The reflective boundary condition (infinite lattice) is used. It is equivalent to a problem involving an infinitely large core composed of a single type of assembly. These calculations are performed by two-dimensional neutron transport codes based on a more accurate neutron transport theory. The neutron flux distribution from these fine-mesh calculations is used to spatially homogenize and condense (with respect to energy) cross-sections and to calculate pin power factors. In this phase, self-shielding corrections are applied to the flux distribution. The homogenized lattice cell data are then used in a simplified core model to which less expensive diffusion theory is applied in the second phase, the nodal calculations.
Lattice Cell Homogenization. In the first phase, the reactor core is decomposed into relatively small core sub-regions, called lattice cells. A lattice cell typically contains a single fuel assembly plus half of the surrounding coolant gap. It is precisely modeled in two-dimensional geometry with materials characterized by fine-group cross-sections (100s of energy group). The reflective boundary condition (infinite lattice) is used. It is equivalent to a problem involving an infinitely large core composed of a single type of assembly. These calculations are performed by two-dimensional neutron transport codes based on a more accurate neutron transport theory. The neutron flux distribution from these fine-mesh calculations is used to spatially homogenize and condense (with respect to energy) cross-sections and to calculate pin power factors. In this phase, self-shielding corrections are applied to the flux distribution. The homogenized lattice cell data are then used in a simplified core model to which less expensive diffusion theory is applied in the second phase, the nodal calculations.- Nodal Calculations. A homogenized lattice cell (one single node) is typically represented by a 20 cm high section of a single fuel assembly. The nodal approach involves a high-order or analytical expansion of the intra-nodal flux shape to achieve a higher degree of accuracy, for a given node size, than the conventional finite difference approach to discretizing the spatial variable. The nodal balance equation is solved within each node, derived from the 3D steady-state multigroup neutron diffusion equation and the nodal balance equation.
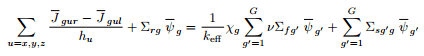 There is a set of equations for the surface average currents instead of directly solving 3D finite difference equations. In approaching surface averaged current, the average flux derivative on a surface is approximated as the derivative of average flux at the surface. It is more efficient to work with the diffusion equation for average flux than the diffusion equation for 3D point-wise fluxes. A transverse integration procedure is often employed to reduce the multi-dimensional equations to a set of coupled one-dimensional equations. The resulting system is then solved on a three-dimensional core model consisting of homogeneous nodes characterized by the generalized equivalence theory (GET) constants generated in the first phase.
There is a set of equations for the surface average currents instead of directly solving 3D finite difference equations. In approaching surface averaged current, the average flux derivative on a surface is approximated as the derivative of average flux at the surface. It is more efficient to work with the diffusion equation for average flux than the diffusion equation for 3D point-wise fluxes. A transverse integration procedure is often employed to reduce the multi-dimensional equations to a set of coupled one-dimensional equations. The resulting system is then solved on a three-dimensional core model consisting of homogeneous nodes characterized by the generalized equivalence theory (GET) constants generated in the first phase. 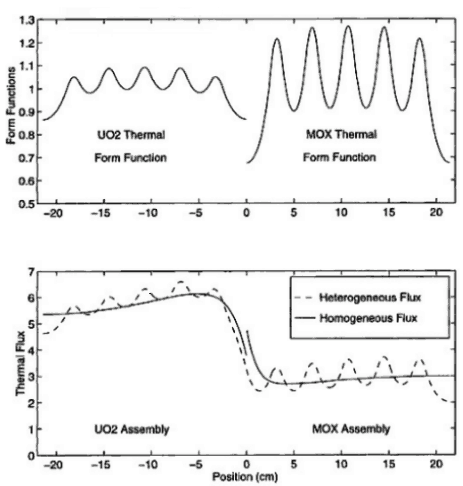 Flux Reconstruction. In this phase, it is necessary to predict the neutron flux in individual fuel rods (pin-by-pin). Therefore we need the heterogeneous solution. The heterogeneous solution is reconstructed from a given homogenized solution. The detailed or heterogeneous flux distribution can be approximated by modulating the smooth nodal solution with the fine-mesh transport solutions using various techniques. The figure shows a superposition of lattice flux (form functions) determined by fine-mesh transport codes with nodal fluxes determined by nodal calculations.
Flux Reconstruction. In this phase, it is necessary to predict the neutron flux in individual fuel rods (pin-by-pin). Therefore we need the heterogeneous solution. The heterogeneous solution is reconstructed from a given homogenized solution. The detailed or heterogeneous flux distribution can be approximated by modulating the smooth nodal solution with the fine-mesh transport solutions using various techniques. The figure shows a superposition of lattice flux (form functions) determined by fine-mesh transport codes with nodal fluxes determined by nodal calculations.
The efficiency of nodal methods is very high and comparable with the finite difference methods. It is very fast and allows us to compute such a huge number of reactor states. It must be added, using this method, one can get only approximate information about the neutron flux in a single node (or coarse-mesh area, usually a single fuel assembly of a 20 cm height). This analysis requires many subsequent calculations of the flux and power distributions for the fuel assemblies while there is no need for detailed distribution within the assembly. For obtaining detailed distribution within the assembly the heterogeneous flux reconstruction must be applied. However, homogenization of fuel assembly properties, required for the nodal method, may cause difficulties when applied to fuel assemblies with many burnable absorber rods due to the very high absorption cross-section (especially with Gd – burnable absorbers) and very strong heterogeneity within the assembly.
These methods are very efficient and accurate when applied to the current Pressurized Water Reactors (PWRs) or Boiling Water Reactors (BWRs).