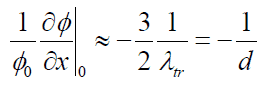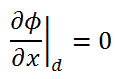Vacuum Boundary Condition

extrapolated length - boundary condition — Neutron flux as a function of position near a free surface according to diffusion theory and transport theory.

The diffusion equation is mostly solved in media with high densities, such as neutron moderators (H₂O, D₂O, or graphite). The problem is usually bounded by air. The mean free path of the neutron in the air is much larger than in the moderator so that it is possible to treat it as a vacuum in neutron flux distribution calculations. The vacuum boundary condition supposes that no neutrons are entering a surface.

If we consider that no neutrons are reflected from the vacuum back to the volume, the following condition can be derived from Fick’s law:

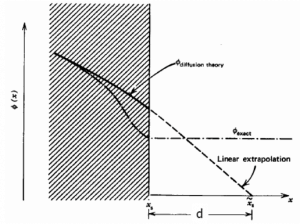
Where d ≈ ⅔ λ_tr is known as the extrapolated length, for homogeneous, weakly absorbing media, an exact solution of the mono-energetic transport equation in this case yields d ≈ 0.7104 λ_tr. The geometric interpretation of the previous equation is that the relative neutron flux near the boundary has a slope of -1/d, i.e., the flux would extrapolate linearly to 0 at a distance d beyond the boundary. This zero flux boundary condition is more straightforward and can be written mathematically as:

If d is not negligible, physical dimensions of the reactor are increased by d, and extrapolated boundary is formulated with dimension R_e = R + d, and this condition can be written as Φ(R + d) = Φ(R_e) = 0.

It may seem the flux goes to 0 at an extrapolated length beyond the boundary. This interpretation is not correct. The flux cannot go to zero in a vacuum because there are no absorbers to absorb the neutrons. The flux only appears to be heading to the zero value at the extrapolation point.

Note that the equation d ≈ 0.7104 λ_tr is applicable to plane boundaries only. The formulas for curved boundaries can differ slightly. However, the difference is small unless the radius of curvature of the boundary is of the same order of magnitude as the extrapolated length.

Typical values of the extrapolated length:

The most common moderators have following diffusion coefficients (for thermal neutrons):

D(H₂O) = 0.142 cm

D(D₂O) = 0.84 cm

D(Be) = 0.416 cm

D(C) = 0.916 cm

The thermal neutron extrapolated lengths are given by:

d ≈ 0.7104 λ_tr = 0.7104 x 3 x D

therefore:

H₂O: d ≈ 0.30 cm

D₂O: d ≈ 1.79 cm

Be: d ≈ 0.88 cm

C: d ≈ 1.95 cm

As can be seen, this approximation is valid when the dimension L of the diffusing medium is much larger than the extrapolated length, L >> d.

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Diffusion Theory