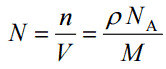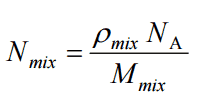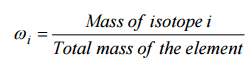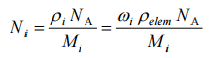The atomic number density (N; atoms/cm3) is the number of atoms of a given type per unit volume (V; cm3) of the material. The atomic number density (N; atoms/cm3) of a pure material having an atomic or molecular weight (M; grams/mol) and the material density (⍴; gram/cm3) is easily computed from the following equation using Avogadro’s number (NA = 6.022×1023 atoms or molecules per mole):
It was written the macroscopic cross-section is derived from microscopic cross-section and the atomic number density (N):
Σ=σ.N
In this equation, the atomic number density plays a crucial role as the microscopic cross-section. In the reactor core, the atomic number density of certain materials (e.g.,, water as the moderator) can be simply changed, leading to certain reactivity changes. To understand the nature of these reactivity changes, we must understand the term the atomic number density.
Atomic Number Density of Mixtures and Compounds
For a chemical compound (mixture) Z or for an isotopic mixture, which is composed of elements or isotopes X and Y, the number (atom) density of the compound is calculated from:
Example – Atomic number densities of boron carbide
A control rod usually contains solid boron carbide with natural boron. Natural boron consists primarily of two stable isotopes,11B (80.1%) and 10B (19.9%). Boron carbide has a density of 2.52 g/cm3.
Determine the atomic number densities of individual constituents.
Density:
MB = 10.8
MC = 12
MMixture = 4 x 10.8 + 1×12 g/mol
NB4C = ρ . Na / MMixture
= (2.52 g/cm3)x(6.02×1023 nuclei/mol)/ (4 x 10.8 + 1×12 g/mol)
= 2.75×1022 molecules of B4C/cm3
NB = 4 x 2.75×1022 atoms of boron/cm3
NC = 1 x 2.75×1022 atoms of carbon/cm3
NB10 = 0.199 x 4 x 2.75×1022 = 2.18×1022 atoms of 10B/cm3
NB11 = 0.801 x 4 x 2.75×1022 = 8.80×1022 atoms of 11B/cm3
NC = 2.75×1022 atoms of 12C/cm3
Example – Fuel enrichment
In nuclear engineering, we are working with the term fuel enrichment. The enrichment may be specified in terms of weight percent or weight fraction, ωi, of isotope i:
The atomic number density of isotope i is:
Most of PWRs use uranium fuel, which is in the form of uranium dioxide (UO2). Typically, the fuel has an enrichment of ω235 = 4% [grams of 235U per gram of uranium] of isotope 235U.
Calculate the atomic number density of 235U (N235U), when:
- the molecular weight of the enriched uranium MUO2 = 237.9 + 32 = 269.9 g/mol
- the uranium density ⍴UO2 = 10.5 g/cm3
NUO2 = ⍴UO2 . NA / MUO2
NUO2 = (10.5 g/cm3) x (6.02×1023 nuclei/mol)/ 269.9
NUO2 = 2.34 x 1022 molecules of UO2/cm3
NU = 1 x 2.34×1022 atoms of uranium/cm3
NO = 2 x 2.34×1022 atoms of oxide/cm3
N235U = ω235.NA.⍴UO2/M235U x (MU/MUO2)
N235U = 0.04 x 6.02×1023 x 10.5 / 235 x 237.9 / 269.9 =9.48 x 1020 atoms of 235U/cm3