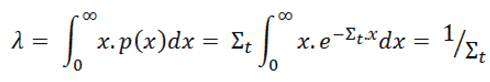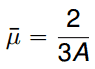Facebook Instagram Youtube Twitter

Mean Free Path

The mean free path or the relaxation length is the path traveled by a neutron between two collisions or interactions. The mean free path is divided from the equation for the probability of the first collision in dx.

From the equation for the probability of the first collision in dx  (P(x)dx = Σtdx . e-Σt.x = Σt e-Σt.x dx), we can calculate the mean free path that is traveled by a neutron between two collisions. The symbol λ usually designates this quantity. It is equal to the average value of x, the distance traveled by a neutron without any interaction, over the interaction probability distribution.

mean free path - equation

whereby one can distinguish λs, λa, λf, etc. This quantity is also known as the relaxation length because it is the distance in which the intensity of the neutrons that have not caused a reaction has decreased with a factor e.

For materials with a high absorption cross-section, the mean free path is very short, and neutron absorption occurs mostly on the material’s surface. This surface absorption is called self-shielding because the outer layers of atoms shield the inner layers.

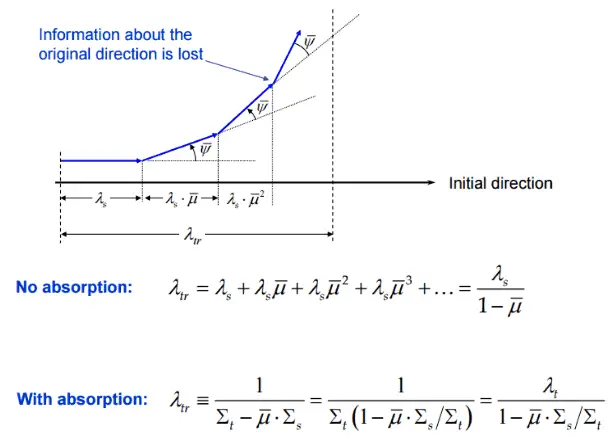
Transport Mean Free Path

The transport means free path (λtr) is an average distance a neutron will move in its original direction after an infinite number of scattering collisions.

diffusion coefficient - angle

is an average value of the cosine of the angle in the lab system at which neutrons are scattered in the medium. It can be calculated for most of the neutron energies as (A is the mass number of target nucleus):

diffusion coefficient - angle2

transport mean free path - graphically

Example – Macroscopic Cross-section and Mean Free Path for boron carbide in control rods

A control rod usually contains solid boron carbide with natural boron. Natural boron consists primarily of two stable isotopes,11B (80.1%) and 10B (19.9%). Boron carbide has a density of 2.52 g/cm3.

Determine the total macroscopic cross-section and the mean free path.

Density:
MB = 10.8
MC = 12
MMixture = 4 x 10.8 + 1×12 g/mol
NB4C = ρ . Na / MMixture
= (2.52 g/cm3)x(6.02×1023 nuclei/mol)/ (4 x 10.8 + 1×12 g/mol)
= 2.75×1022 molecules of B4C/cm3

NB = 4 x 2.75×1022 atoms of boron/cm3
NC = 1 x 2.75×1022 atoms of carbon/cm3

NB10 = 0.199 x 4 x 2.75×1022 = 2.18×1022 atoms of 10B/cm3
NB11 = 0.801 x 4 x 2.75×1022 = 8.80×1022 atoms of 11B/cm3
NC = 2.75×1022 atoms of 12C/cm3

the microscopic cross-sections

σt10B = 3843 b of which σ(n,alpha)10B = 3840 b
σt11B = 5.07 b
σt12C = 5.01 b

the macroscopic cross-section

ΣtB4C = 3843×10-24 x 2.18×1022 + 5.07×10-24 x 8.80×1022 + 5.01×10-24 x 2.75×1022
= 83.7 + 0.45 + 0.14 = 84.3 cm-1

the mean free path

λt = 1/ΣtB4C = 0.012 cm = 0.12 mm (compare with B4C pellets diameter in control rods which may be around 7mm)
λa ≈ 0.12 mm

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See previous:

See above:

Neutron Nuclear Reactions

See next: