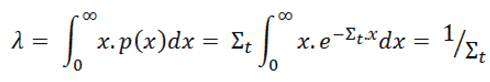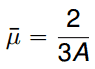Facebook Instagram Youtube Twitter

Transport Mean Free Path

From the equation for the probability of the first collision in dx  (P(x)dx = Σtdx . e-Σt.x = Σt e-Σt.x dx), we can calculate the mean free path that is traveled by a neutron between two collisions. This quantity is usually designated by the symbol λ, and it is equal to the average value of x, the distance traveled by a neutron without any interaction, over the interaction probability distribution.

mean free path - equation

whereby one can distinguish λs, λa, λf, etc. This quantity is also known as the relaxation length because it is the distance in which the intensity of the neutrons that have not caused a reaction has decreased with a factor e.

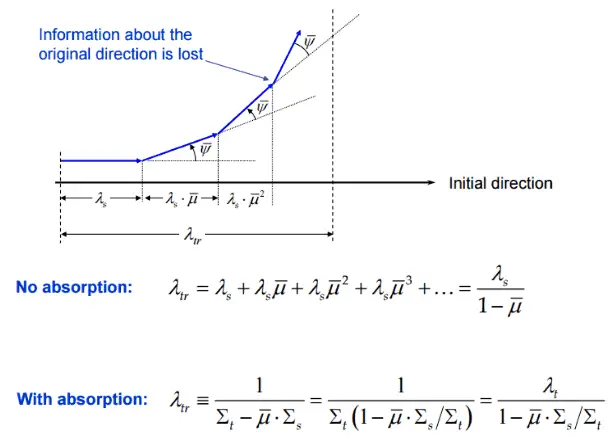
The transport means free path (λtr) is an average distance a neutron will move in its original direction after an infinite number of scattering collisions.

diffusion coefficient - angle

is an average value of the cosine of the angle in the lab system at which neutrons are scattered in the medium. It can be calculated for most of the neutron energies as (A is the mass number of target nucleus):

diffusion coefficient - angle2

transport mean free path - graphically

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Reactor Physics