Neutron Capture Cross-section
The radiative capture cross-section represents the likelihood of a neutron radiative capture as σγ. As usual, the cross-section can be divided into three regions according to the incident neutron energy.
- 1/v Region
- Resonance Region
- Fast Neutrons Region
1/v Region
In the common case, the cross-section is usually much larger at low energies than at high energies. For thermal neutrons (in 1/v region), radiative capture cross-sections also increase as the neutron’s velocity (kinetic energy) decreases. Therefore the 1/v Law can be used to determine a shift in capture cross-section if the neutron is in equilibrium with a surrounding medium. This phenomenon is because the nuclear force between the target nucleus and the neutron has a longer time to interact.
Resonance Region
The largest cross-sections are usually at neutron energies that lead to long-lived states of the compound nucleus. The compound nuclei of these certain energies are called nuclear resonances, and their formation is typical in the resonance region. The widths of the resonances increase in general with increasing energies. At higher energies, the widths may reach the order of the distances between resonances, and then no resonances can be observed. The narrowest resonances are usually compound states of heavy nuclei (such as fissionable nuclei).
Since the mode of decay of the compound nucleus does not depend on the way the compound nucleus was formed, the nucleus sometimes emits a gamma-ray (radiative capture) or sometimes emits a neutron (scattering). To understand how a nucleus will stabilize itself, we have to understand the behavior of the compound nucleus.
The compound nucleus emits a neutron only after one neutron obtains energy in collision with another nucleon greater than its binding energy in the nucleus. It has some delay because the excitation energy of the compound nucleus is divided among several nucleons. The average time that elapses before a neutron can be emitted is much longer for nuclei with many nucleons than when only a few nucleons are involved. It is a consequence of sharing the excitation energy among a large number of nucleons.
This is why the radiative capture is comparatively unimportant in light nuclei but becomes increasingly important in heavier nuclei.
The lifetime of a compound nucleus is inversely proportional to its total width. Narrow resonances, therefore, correspond to capture, while the wider resonances are due to scattering.
Example:Source: R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
The first resonance in 238U at 6.67 eV, which corresponds to the first virtual level in 239U, has a total width of only 0.027 eV, and the mean life of this state is 2.4×10-14s. By contrast, the resonance observed at 443 keV in 16O, which corresponds to the first virtual state in 17O, has a total width of 41 keV, giving a mean lifetime of 1.5×10-21s. Thus it is highly likely that the compound state in 239U decays at least to some extent by gamma-ray emission, while the compound state in 17O must decay primarily by nucleon emission. The 443-keV resonance in 16O is clearly a scattering resonance, whereas the 6.67-eV resonance in 238U is in part a capture resonance.
σγ
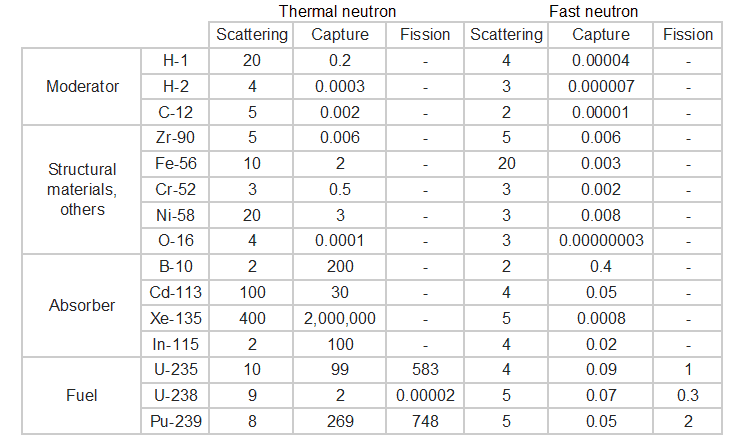
Table of cross-sections.
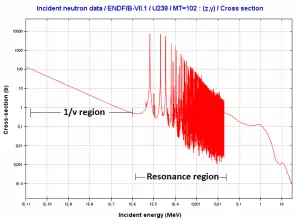Radiative Capture Cross-section – region of resonances of 238U nuclei.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
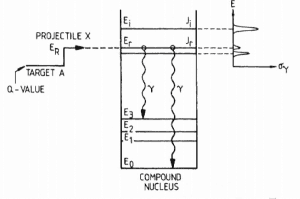
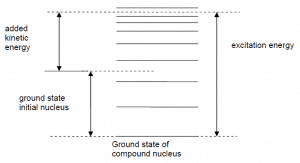Energy levels of compound state. For neutron absorption reaction on 238U the first resonance E1 corresponds to the excitation energy of 6.67eV. E0 is a base state of 239U.
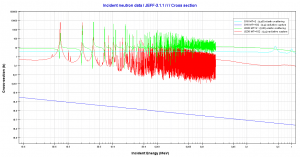Radiative capture and elastic scattering cross-sections in 16O and 238U.Doppler Broadening
In general, Doppler broadening is the broadening of spectral lines due to the Doppler effect caused by a distribution of kinetic energies of molecules or atoms. In reactor physics, a particular case of this phenomenon is the thermal Doppler broadening of resonances caused by the thermal motion of the target particle in the nuclear fuel.
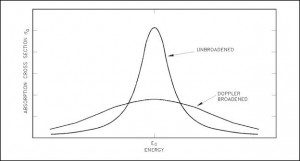
The Doppler broadening of resonances is a very important phenomenon, which improves reactor stability. The prompt temperature coefficient of most thermal reactors is negative, owing to a nuclear Doppler effect. Although the absorption cross-section depends significantly on incident neutron energy, the shape of the cross-section curve also depends on the target temperature.
Nuclei are located in atoms that are themselves in continual motion owing to their thermal energy. As a result of these thermal motions, neutrons impinging on a target appear to the nuclei in the target to have a continuous spread in energy. This, in turn, affects the observed shape of resonance. The resonance becomes shorter and wider than when the nuclei are at rest.
Although the shape of a resonance changes with temperature, the total area under the resonance remains essentially constant. But this does not imply constant neutron absorption. Despite the constant area under resonance, a resonance integral, which determines the absorption, increases with increasing target temperature. This, of course, decreases coefficient k (negative reactivity is inserted).
Fast Neutrons Region
The radiative capture cross-section at energies above the resonance region drops rapidly to very small values. This rapid drop is caused by the compound nucleus, which is formed in more highly excited states. In these highly excited states, it is more likely that one neutron obtains energy in collision with another nucleon greater than its binding energy in the nucleus. The neutron emission becomes dominant, and gamma decay becomes less important. Moreover, at high energies, the inelastic scattering and (n,2n) reaction are highly probable at the expense of both elastic scattering and radiative capture.
Cross-sections of key isotopes
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
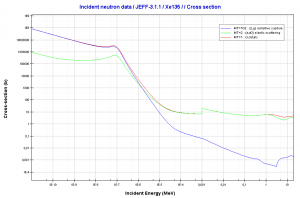Xenon – 135. Neutron absorption and scattering. Comparison of cross-sections.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library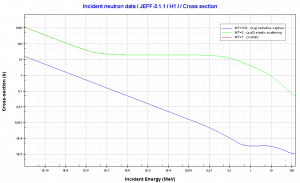
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
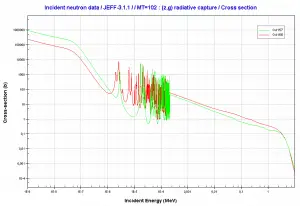Gadolinium 155 and 157. Comparison of radiative capture cross-sections.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
