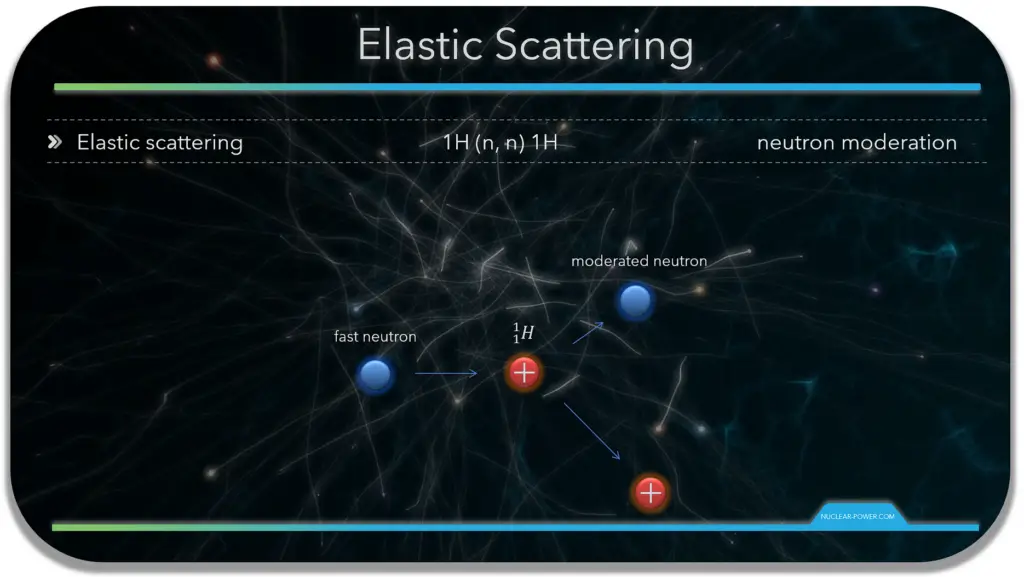
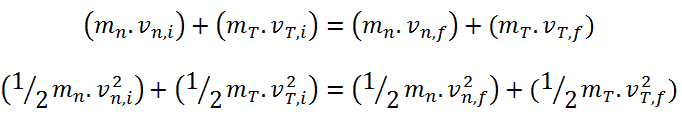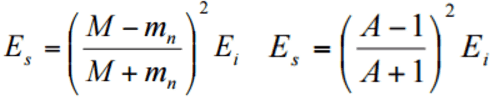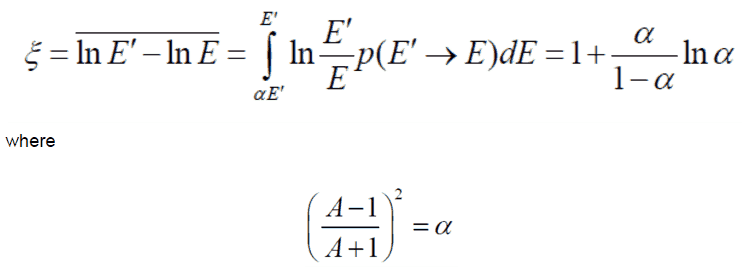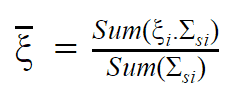The elastic scattering conserves both momentum and kinetic energy of the “system”. It may be modeled as a billiard ball collision between a neutron and a nucleus.
There is usually some transfer of kinetic energy from the incident neutron to the target nucleus. The target nucleus gains the exact amount of kinetic energy that the neutron loses. This interaction can occur via compound nucleus formation, but in the case of elastic scattering, a neutron emission returns the compound nucleus to the ground state of the original nucleus. Therefore the initial and final neutrons do not need to be necessarily the same.
The elastic scattering can occur by way of two interaction mechanisms:
- Potential scattering. In potential scattering, the neutron and the nucleus interact without neutron absorption and a compound nucleus. In fact, the incident neutron does not necessarily have to “touch” the nucleus, and the neutron is scattered by the short-range nuclear forces when it approaches close enough to the nucleus. Potential scattering occurs with incident neutrons that have an energy of up to about 1 MeV. It may be modeled as a billiard ball collision between a neutron and a nucleus.
- Compound-elastic scattering. In some cases, if the kinetic energy of an incident neutron is just right to form a resonance, the neutron may be absorbed, and a compound nucleus may be formed. This interaction is more unusual and is also known as resonance elastic scattering. Due to the formation of the compound nucleus, the initial and final neutron are not the same.
Conservation of momentum and kinetic energy
where:
mn = mass of the neutron
mT = mass of the target nucleus T
vn,i = initial neutron speed
vn,f = final neutron speed
vT,i = initial target speed
vT,f = final target speed
Key Characteristics of Elastic Scattering
- Elastic scattering is the most important process for slowing down neutrons.
- The total kinetic energy of the system is conserved in the elastic scattering.
- In this process, energy lost by the neutron is transferred to the recoiling nucleus.
- Maximum energy transfer occurs with a head-on collision.
- The kinetic energy of the recoiled nucleus depends on the recoiled angle φ of the nucleus.
- Elastic scattering cross-sections for light elements are more or less independent of neutron energy up to 1 MeV.
- For intermediate and heavy elements, the elastic cross-section is constant at low energy with some specifics at higher energy.
- A good approximation is, σs = const, for all elements that are of importance.
- At low energy, σs can be described by the one-level Breit-Wigner formula.
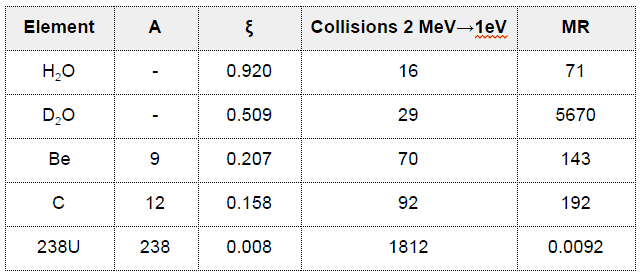
- Nearly all elements have scattering cross-sections in the range of 2 to 20 barns.
- The important exception is for water and heavy water.
- If the kinetic energy of an incident neutron is large compared with the chemical binding energy of the atoms in a molecule, the chemical bound can be ignored.
- If the kinetic energy of an incident neutron is of the order or less than the chemical binding energy, the cross-section of the molecule is not equal to the sum of cross-sections of its individual nuclei.
- The scattering of slow neutrons by molecules is greater than by free nuclei.
- Therefore one nucleus microscopic cross-section does not describe the process correctly, while the macroscopic cross-section (Σs) has a precise meaning.
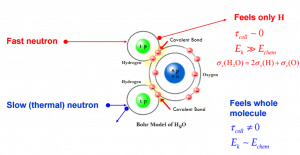The scattering of slow neutrons by molecules is greater than by free nuclei.
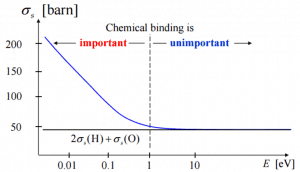
If the kinetic energy of an incident neutron is of the order or less than the chemical binding energy, the cross-section of the molecule is not equal to the sum of cross-sections of its individual nuclei.
Elastic Scattering Cross-section
To be an effective moderator, the probability of elastic reaction between neutron and the nucleus must be high. In terms of cross-sections, the elastic scattering cross-section of a moderator’s nucleus must be high.
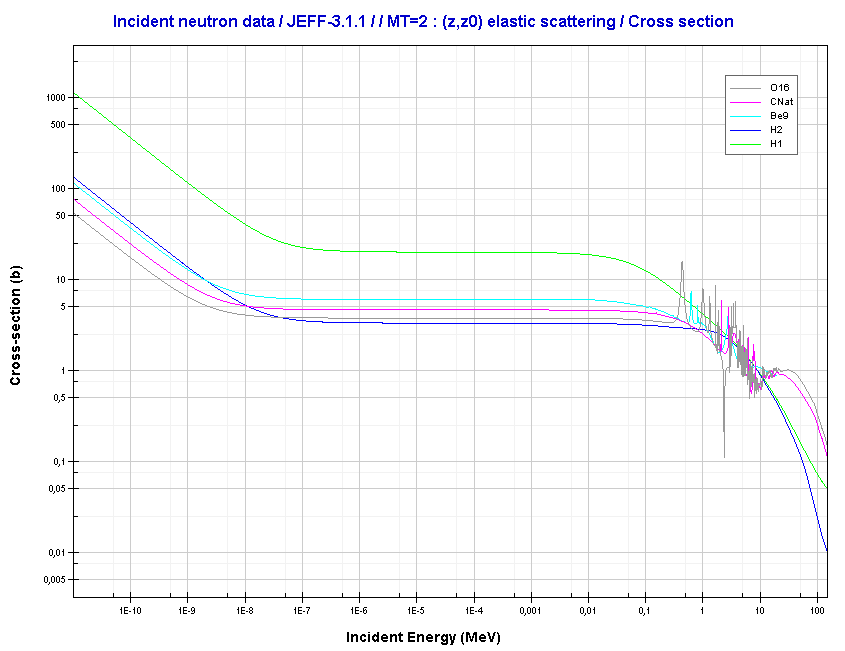
Elastic scattering cross-sections for light elements are more or less independent of neutron energy up to 1 MeV.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
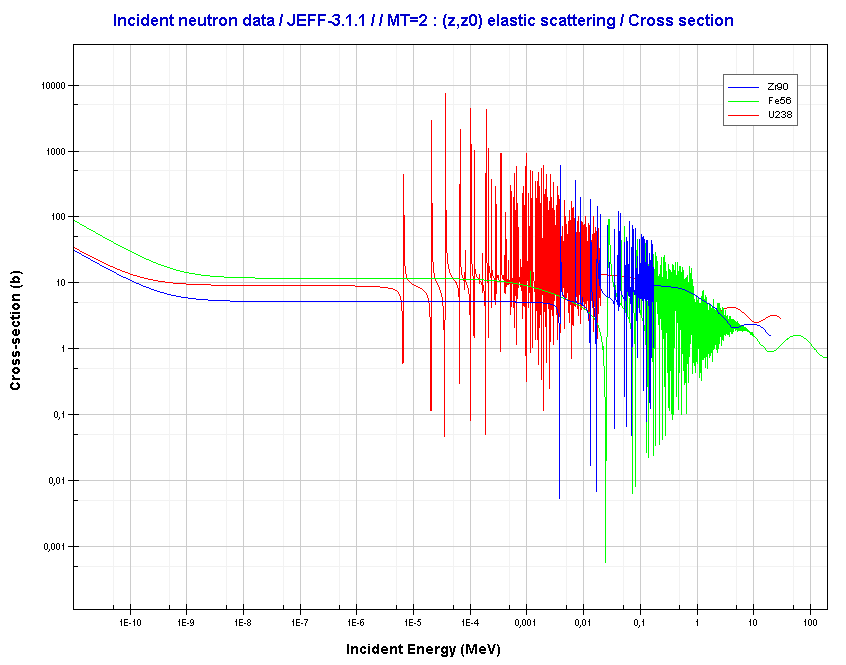
For intermediate and heavy elements, the elastic cross-section is constant at low energy with some specifics at higher energy.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
Elastic Scattering and Neutron Moderators
As can be seen, a high elastic scattering cross-section is important but does not comprehensively describe moderators’ capabilities. To describe the capabilities of a material to slow down neutrons, three new material variables must be defined:
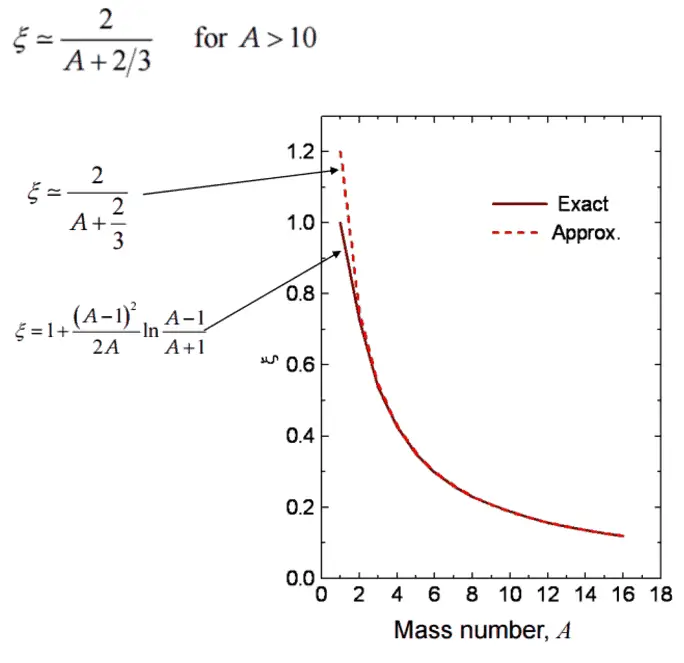
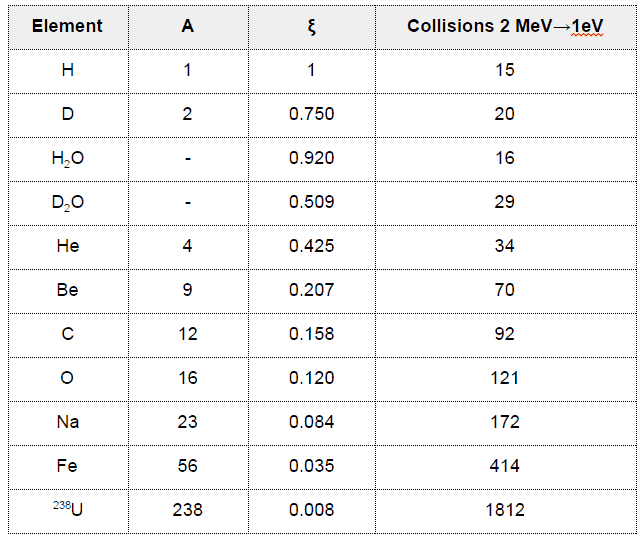
- The Average Logarithmic Energy Decrement (ξ)
- The Macroscopic Slowing Down Power (MSDP)
- The Moderating Ratio (MR)
Key properties of neutron moderators:
- the high cross-section for neutron scattering
- high energy loss per collision
- the low cross-section for absorption
- high melting and boiling point
- high thermal conductivity
- high specific heat capacity
- low viscosity
- low activity
- low corrosive
- cheap
where A is the atomic mass number.
In the case of the hydrogen (A = 1) as the target nucleus, the incident neutron can be completely stopped. But this works when the direction of the neutron is completely reversed (i.e., scattered at 180°). In reality, the direction of scattering ranges from 0 to 180 °, and the energy transferred also ranges from 0% to maximum. Therefore, the average energy of the scattered neutron is taken as the average of energies with scattering angles 0 and 180°.
Moreover, it is useful to work with logarithmic quantities. Therefore one defines the logarithmic energy decrement per collision (ξ) as a key material constant describing energy transfers during a neutron slowing down. ξ is not dependent on energy, only on A and is defined as follows:
For heavy target nuclei, ξ may be approximated by the following formula:
From these equations, it is easy to determine the number of collisions required to slow down a neutron from, for example, from 2 MeV to 1 eV.
Example:
Determine the number of collisions required for thermalization for the 2 MeV neutrons in the carbon.
ξCARBON = 0.158
N(2MeV → 1eV) = ln 2⋅106/ξ =14.5/0.158 = 92
For a mixture of isotopes:
MSDP = ξ . Σs
The MSDP describes the ability of a given material to slow down neutrons and indicates how rapidly a neutron will slow down in the material. Still, it does not fully reflect the effectiveness of the material as a moderator. In fact, the material with high MSDP can slow down neutrons with high efficiency, but it can be a poor moderator because of its high probability of absorbing neutrons. It is typical, for example, for boron, which has a high slowing down power but is absolutely inappropriate as a moderator.
The complete measure of the effectiveness of a moderator is the Moderating Ratio (MR), where:
MR = ξ . Σs/Σa
Therefore a higher ratio of MSDP to absorption cross-sections ξ . Σs/Σa is desirable for effective moderation. This ratio is called the moderating ratio – MR and can be used as a criterion for comparing different moderators.
Examples:
- Light water has the highest ξ and σs among the moderators (resulting in the highest MSDP) shown in the table. Still, its moderating ratio is low due to its relatively higher absorption cross-section.
- On the other hand, heavy water has lower ξ and σs, but it has the highest moderating ratio owing to its lowest neutron absorption cross-section.
- Graphite has much heavier nuclei than hydrogen in water. Even though graphite has much lower ξ and σs, it is a better moderator than light water due to its lower absorption cross-section than light water.
