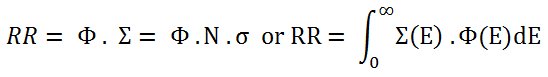The section on the neutron cross-section determined the probability of a neutron undergoing a specific neutron-nuclear reaction. It was determined the mean free path of neutrons in the material under specific conditions. These parameters influence the criticality of the reactor core. In other words, we do not know anything about the power level of the reactor core. If we want to know the reactor core’s reaction rate or thermal power, it is necessary to know how many neutrons are traveling through the material.
It is convenient to consider the neutron density, the number of neutrons existing in one cubic centimeter. The symbol n represents the neutron density with units of neutrons/cm3. In reactor physics, the neutron flux is more likely used because it expresses better the total path length covered by all neutrons. Their velocity determines the total distance these neutrons can travel each second. The neutron flux density value is calculated as the neutron density (n) multiplied by neutron velocity (v).
Ф = n.v
where:
Ф – neutron flux (neutrons.cm-2.s-1)
n – neutron density (neutrons.cm-3)
v – neutron velocity (cm.s-1)
The neutron flux, the number of neutrons crossing through some arbitrary cross-sectional unit area in all directions per unit time, is a scalar quantity. Therefore it is also known as the scalar flux. The expression Ф(E).dE is the total distance traveled during one second by all neutrons with energies between E and dE located in 1 cm3.
The connection to the reaction rate, respectively, the reactor power is obvious. Knowledge of the neutron flux (the total path length of all the neutrons in a cubic centimeter in a second) and the macroscopic cross-sections (the probability of having an interaction per centimeter path length) allows us to compute the rate of interactions (e.g.,, rate of fission reactions). The reaction rate (the number of interactions taking place in that cubic centimeter in one second) is then given by multiplying them together:
where:
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross-section (cm2)
N – atomic number density (atoms.cm-3)
Neutron Flux and Intensity – Examples
We have to distinguish between the neutron flux and the neutron intensity. Although both physical quantities have the same units, namely, neutrons.cm-2.s-1, their physical interpretations are different. In contrast to the neutron flux, the neutron intensity is the number of neutrons crossing through some arbitrary cross-sectional unit area in a single direction per unit time (a surface is perpendicular to the direction of the beam). The neutron intensity is a vector quantity.
Solution:
Multiplying the reaction rate per unit volume (RR = Ф . Σ) by the total volume of the core (V) gives us the total number of reactions occurring in the reactor core per unit time. But we also know the amount of energy released per one fission reaction to be about 200 MeV/fission. Now, it is possible to determine the energy release rate (power) due to the fission reaction. The following equation gives it:
P = Ф . Σf . Er . V = Ф . NU235 . σf235 . Er . V
where:
P – reactor power (MeV.s-1)
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
Er – the average recoverable energy per fission (MeV / fission)
V – total volume of the core (m3)
The amount of fissile 235U per the volume of the reactor core.
m235 [g/core] = 100 [metric tons] x 0.02 [g of 235U / g of U] . 106 [g/metric ton] = 2 x 106 grams of 235U per the volume of the reactor core
The atomic number density of 235U in the volume of the reactor core:
N235 . V = m235 . NA / M235
= 2 x 106 [g 235 / core] x 6.022 x 1023 [atoms/mol] / 235 [g/mol]
= 5.13 x 1027 atoms / core
The microscopic fission cross-section of 235U (for thermal neutrons):
σf235 = 585 barns
The average recoverable energy per 235U fission:
Er = 200.7 MeV/fission
Moreover, it will be assumed. The recycled plutonium contains only the fissile 239Pu. In reality, MOX fuel always contains significant amounts of higher isotopes – 240Pu, 241Pu, and 242Pu. The presence of these amounts will be neglected in this example.
A typical thermal reactor contains about 100 tons of fuel (HM – heavy metal). If the reactor power is 3000MWth, determine the reaction rate and the average core thermal flux.
Solution:
Multiplying the reaction rate per unit volume (RR = Ф . Σ) by the total volume of the core (V) gives us the total number of reactions occurring in the reactor core per unit time. But we also know the amount of energy released per one fission reaction is about 207 MeV/fission. Now, it is possible to determine the energy release rate (power) due to the fission reaction. The following equation gives it:
P = Ф . Σf . Er . V = Ф . NPu239 . σf239 . Er . V
where:
P – reactor power (MeV.s-1)
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
Er – the average recoverable energy per fission (MeV / fission)
V – total volume of the core (m3)
The amount of fissile 239Pu per the volume of the reactor core.
m239 [g/core] = 100 [metric tons] x 0.02 [g of 239Pu / g of fuel] . 106 [g/metric ton] = 4 x 106 grams of 239Pu per the volume of the reactor core
The atomic number density of 239Pu in the volume of the reactor core:
N239 . V = m239 . NA / M239
= 4 x 106 [g 239 / core] x 6.022 x 1023 [atoms/mol] / 239 [g/mol]
= 10.1 x 1027 atoms / core
The microscopic fission cross-section of 235U (for thermal neutrons):
σf239 = 750 barns
The average recoverable energy per 239Pu fission:
Er = 207 MeV/fission
Neutron Flux – Uranium vs. MOX
Note that there is a difference between neutron fluxes in the uranium fueled core and the MOX fueled core. The average neutron flux in the first example, in which the neutron flux in a uranium-loaded reactor core was calculated, was 3.11 x 1013 neutrons.cm-2.s-1. Compared to this value, the average neutron flux in 100% MOX fueled core is about 2.6 times lower (1.2 x 1013 neutrons.cm-2.s-1), while the reaction rate remains almost the same. This fact is of importance in the reactor core design and the design of reactivity control. It is primarily caused by:
- Higher fission cross-section of 239Pu. The fission cross-section is about 750 barns in comparison with 585 barns for 235U.
- Higher energy release per one fission event. A MOX core does not require the neutron flux of the uranium fueled core to generate the same energy.
- Larger fissile loading. The main reason is the larger fissile loading. In MOX fuels, there is a relatively high buildup of 240Pu and 242Pu. Due to the relatively lower fission-to-capture ratio, there is a higher accumulation of these isotopes, parasitic absorbers, resulting in a reactivity penalty. In general, the average regeneration factor η is lower for 239Pu fuel than for 235U fuel. Therefore the MOX fuel requires a larger fissile loading to achieve the same initial reactivity at the beginning of the fuel cycle.
The relatively lower average neutron flux in MOX cores has the following consequences on reactor core design:
- Because of the lower neutron flux and the larger thermal absorption cross-section for 239Pu, reactivity worth of control rods, chemical shim (PWRs), and burnable absorbers is less with MOX fuel.
- The high fission cross-section of 239Pu and the lower neutron flux lead to greater power peaking in fuel rods that are located near water gaps or when MOX fuel is loaded with uranium fuel together.
Neutron Flux and Fuel Burnup
In a power reactor over a relatively short period (days or weeks), the atomic number density of the fuel atoms remains relatively constant. Therefore, the average neutron flux remains constant in this short period when a reactor is operated at a constant power level. On the other hand, the atomic number densities of fissile isotopes over months decrease due to the fuel burnup, and the macroscopic cross-sections decrease. This result is slow to increase in the neutron flux to keep the desired power level.