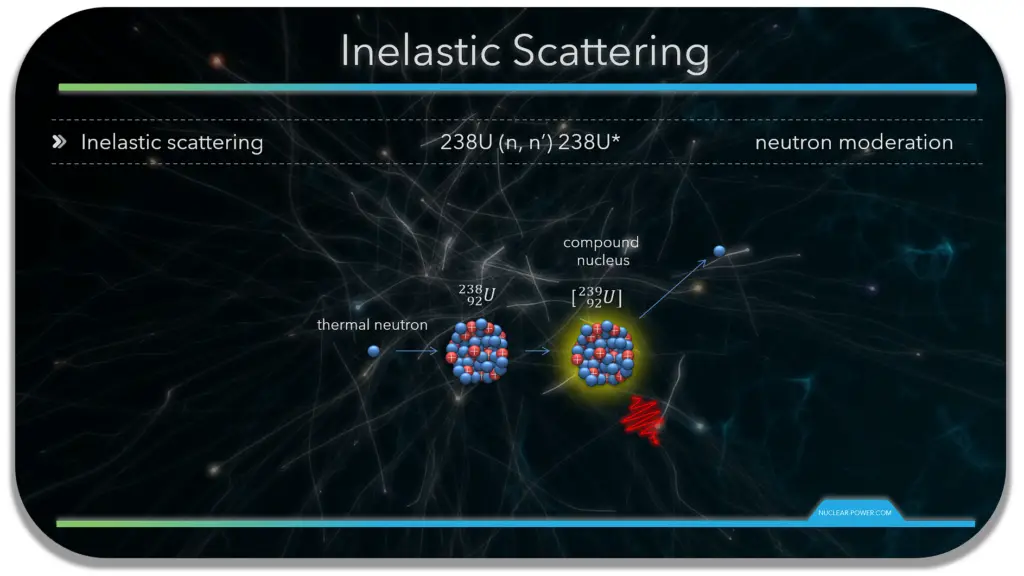
Generally, a neutron scattering reaction occurs when a target nucleus emits a single neutron after a neutron-nucleus interaction. Besides, in an inelastic scattering reaction between a neutron and a target nucleus, some energy of the incident neutron is absorbed into the recoiling nucleus and the nucleus remains in the excited state. Thus while momentum is conserved in an inelastic collision, the kinetic energy of the “system” is not conserved.
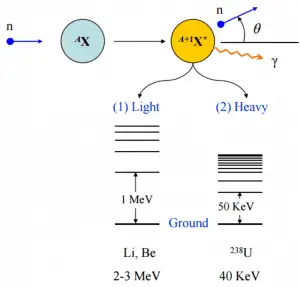
In inelastic neutron scattering, the incident neutron is absorbed by the target nucleus, and the interaction takes place via compound nucleus formation. The compound nucleus emits then a neutron of lower kinetic energy, which leaves the original nucleus in an excited state. The nucleus gives up excitation energy by emitting one or more gamma rays to reach its ground state. In comparison to elastic scattering reactions, it is not easy to write an expression for the average energy loss of inelastic scattering reactions because it depends on the energy levels within the target nucleus.
Inelastic scattering occurs above threshold energy. This threshold energy is higher than the energy of the first excited state of the target nucleus (due to the laws of conservation), and the following formula gives it:
Et = ((A+1)/A)* ε1
where Et is known as the inelastic threshold energy and ε1 is the energy of the first excited state.
In general, the energy of the first excited state of nuclei decreases with increasing mass number. Therefore an inelastic scattering plays an important role in slowing down neutrons, especially at high energies and by heavy nuclei. In calculations of a reactor, inelastic scattering by light nuclei (such as oxygen with Et = 6.42 MeV) can ordinarily be ignored. Moreover, the hydrogen nucleus does not have excited states, so only an elastic scattering reaction can occur in that case.
On the other hand, an inelastic scattering by uranium nuclei (especially by 238U) must be included. 238U is a major component of nuclear fuel in commercial power reactors. Therefore its scattering data are one of the most important data in the neutron transport calculations in the reactor core.
See also: Inelastic Scattering and Capture Cross-section Data of Major Actinides in the Fast Neutron Region, INDC(NDS)-0597. IAEA, 12/2012.
Key Characteristics of Inelastic Scattering
- During an inelastic scattering, the neutron is absorbed and then re-emitted.
- The reaction occurs via the compound nucleus.
- While momentum is conserved in an inelastic collision, the kinetic energy of the “system” is not conserved.
- Some energy of the incident neutron is absorbed into the recoiling nucleus, and the nucleus remains in the excited state.
- The nucleus gives up excitation energy by emitting one or more gamma rays.
- General notation: A(n, n’)A* or A(n, 2n’)B; Example: 14O(n, n’)14O*.
- Inelastic scattering is a threshold reaction and occurs above threshold energy.
- Inelastic scattering cross-section is relatively small for light nuclei.
- For hydrogen nuclei, inelastic scattering does not occur because it does not have excited states.
- Inelastic scattering plays an important role in slowing down neutrons, especially at high energies and by heavy nuclei (e.g.,, 238U).
- Inelastic scattering may be significant for heterogeneous reactors with highly enriched fuel (e.g.,, in fast neutron reactors).
Inelastic Scattering Cross-section
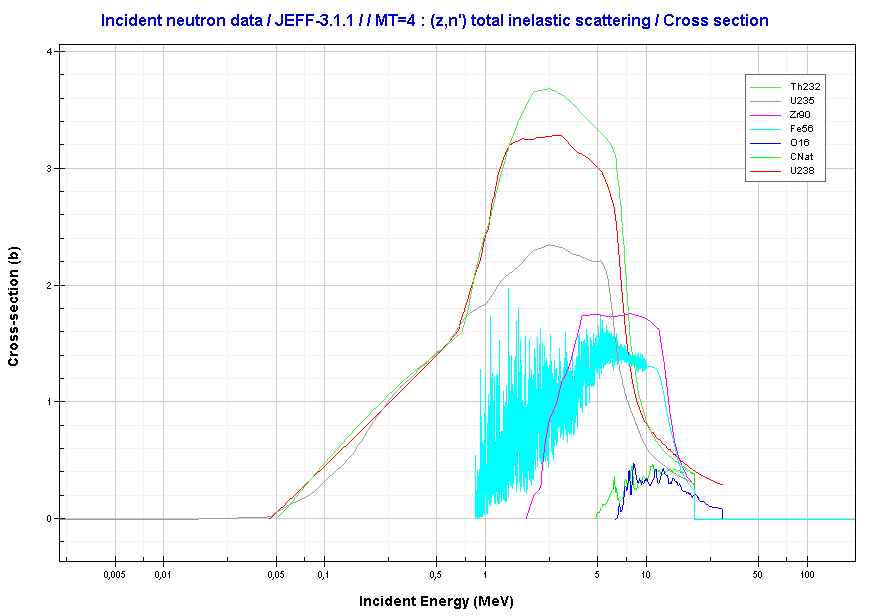Inelastic neutron scattering cross sections.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
