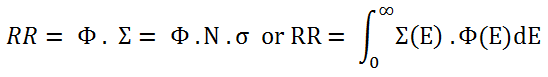Knowledge of the neutron flux (the total path length of all the neutrons in a cubic centimeter in a second) and the macroscopic cross sections (the probability of having an interaction per centimeter path length) allows us to compute the rate of interactions (e.g., rate of fission reactions). The reaction rate (the number of interactions taking place in that cubic centimeter in one second) is then given by multiplying them together:
where:
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
The reaction rate for various types of interactions is found from the appropriate cross-section type:
- Σt . Ф – total reaction rate
- Σa . Ф – absorption reaction rate
- Σc . Ф – radiative capture reaction rate
- Σf . Ф – fission reaction rate
Reaction Rate and Reactor Power Calculation
Multiplying the reaction rate per unit volume (RR = Ф . Σ) by the total volume of the core (V) gives us the total number of reactions occurring in the reactor core per unit time. But we also know the amount of energy released per one fission reaction to be about 200 MeV/fission. Now, it is possible to determine the rate of energy release (power) due to the fission reaction. It is given by following equation:
P = RR . Er . V = Ф . Σf . Er . V = Ф . NU235 . σf235 . Er . V
where:
P – reactor power (MeV.s-1)
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
Er – the average recoverable energy per fission (MeV / fission)
V – total volume of the core (m3)
Example – Reaction Rate and Reactor Power
A typical thermal reactor contains about 100 tons of uranium with an average enrichment of 2% (do not confuse it with the enrichment of the fresh fuel). If the reactor power is 3000MWth, determine the reaction rate and the average core thermal flux.
Solution:
The amount of fissile 235U per the volume of the reactor core.
m235 [g/core] = 100 [metric tons] x 0.02 [g of 235U / g of U] . 106 [g/metric ton] = 2 x 106 grams of 235U per the volume of the reactor core
The atomic number density of 235U in the volume of the reactor core:
N235 . V = m235 . NA / M235
= 2 x 106 [g 235 / core] x 6.022 x 1023 [atoms/mol] / 235 [g/mol]
= 5.13 x 1027 atoms / core
The microscopic fission cross-section of 235U (for thermal neutrons):
σf235 = 585 barns
The average recoverable energy per 235U fission:
Er = 200.7 MeV/fission